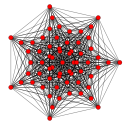
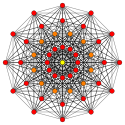
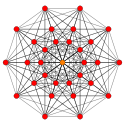
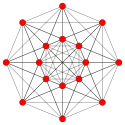
7-demicube
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Partai Reformasi Estonia Eesti ReformierakondKetua umumTaavi RõivasDibentuk18 November 1994Kantor pusatTõnismägi 9 Tallinn 10119Sayap pemudaPemuda Partai Reformasi EstoniaKeanggotaan (2014)12,972IdeologiLiberalisme[1] Classical liberalism[2]Posisi politikTengah-kanan[3]Afiliasi EropaAlliance of Liberals and Democrats for EuropeAfiliasi internasionalLiberal InternationalKelompok Parlemen EropaAlliance of Liberals and Democrats for EuropeWarnaKuning dan biruRiigi...

سانت إغناس الإحداثيات 45°51′57″N 84°43′33″W / 45.865833333333°N 84.725833333333°W / 45.865833333333; -84.725833333333 تاريخ التأسيس 1671 سبب التسمية إغناطيوس دي لويولا تقسيم إداري البلد الولايات المتحدة[1][2] التقسيم الأعلى مقاطعة ماكيناك عاصمة لـ مقاطعة ماكيناك...

Tortequesne Kommun Vapen Land Frankrike Region Hauts-de-France Departement Pas-de-Calais Arrondissement Arras Kanton Vitry-en-Artois Koordinater 50°17′N 3°2′Ö / 50.283°N 3.033°Ö / 50.283; 3.033 Yta 3,37 km²[1] Folkmängd 839 (2020-01-01)[2] Befolkningstäthet 249 invånare/km² Postnummer 62490 INSEE 62825 Geonames 2972402 OSM-karta 1208545 Kommunens läge i regionen Hauts-de-France i Frankrike Kommunens läge i regionen Hauts-de-France ...

American basketball and volleyball player Natalie WilliamsLas Vegas AcesPositionGeneral ManagerPersonal informationBornNovember 30, 1970 (1970-11-30) (age 52)Long Beach, California, U.S.Listed height6 ft 2 in (1.88 m)Listed weight210 lb (95 kg)Career informationHigh schoolTaylorsville (Taylorsville, Utah)CollegeUCLA (1990–1994)WNBA draft1999: 1st round, 3rd overall pickSelected by the Utah StarzzPlaying career1996–2005Career history1996–1998Portland Po...

Menara Kyoto京都タワーLocation within JepangInformasi umumJenisMenara observasiLokasi721-1 Karasuma-doriHigashi Shiokoji-choShimogyō-ku, Kyoto 600-8216Mulai dibangun1963Rampung1964Pembukaan28 Desember 1964Biaya¥380 juta($1,056 juta pada tahun 1963)[1]TinggiMenara antena131 meter (430 ft)Desain dan konstruksiArsitekMakoto Tanahashi Menara Kyoto (京都タワーcode: ja is deprecated , Kyōto-tawā) adalah sebuah menara observasi yang terletak di Kyoto, Jepang. Menara baja i...

منظر لجبال الإلبه بالقرب من مدينة راتن Rathen. جبال الإلبه الحجرية الرملية (بالإنجليزية: Elbe Sandstone Mountains) هي جبال أغلبها من الحجر الرملي على صعيد نهر الإلبه الذي ينبع في أرض التشيك، ثم يمر بالأراضي الألمانية المنخفضة نحو الشمال الغربي حتى يصب في بحر الشمال عند مدينة هامبورغ.[1&#...

Уконяп. 右近 Народилася X ст.ЯпоніяПомерла X ст.Країна ЯпоніяНаціональність японкаДіяльність поетка, письменницяЗнання мов японськаЖанр вакаРід Південні ФудзівараБатько Фудзівара но Суенава Медіафайли у Вікісховищі Укон (*右近, X ст.) — середньовічна японська �...

Filipino pastor and religious leader In this Philippine name, the middle name or maternal family name is Carreon and the surname or paternal family name is Quiboloy. Apollo QuiboloyQuiboloy in 2019TitleExecutive Pastor of the Kingdom of Jesus Christ Datu PamulinganPersonalBorn (1950-04-25) April 25, 1950 (age 73)Dumanlas, Buhangin, Davao City, PhilippinesReligionChristianityDenominationRestorationistChurchUnited Pentecostal Church (former)Kingdom of Jesus ChristFounder ofKi...

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Maio de 2023) O presidente da República Venceslau Brás declara guerra contra o Império Alemão e seus aliados. Ao seu lado, o ex-presidente da República e ministro interino das Relações Exteriores, Nilo Peçanha, e o presidente de Mi...

Nahdlatul UlamaLambang Nahdlatul Ulama, digambar pertama kali oleh K.H. Ridwan Abdullah, kemudian disempurnakan lagi berdasarkan hasil Musyawarah Nasional ke-33 Tahun 2015 di JombangSingkatanNUTanggal pendirian16 Rajab 1344 H (31 Januari 1926; 97 tahun lalu (1926-01-31)PendiriHasyim Asy'ariDidirikan diKabupaten Jombang, Jawa Timur, Hindia BelandaTipeOrganisasi keagamaanTujuanBerlakunya ajaran Islam yang menganut pemahaman ahlussunnah wal-jama'ah bermazhab Asy'ariyah untuk terwujudnya tat...

Monument érigé sous le régime Kérékou aux victimes du coup d'état manqué du 16 janvier 1977. Place des martyrs, Cotonou, Bénin La tentative de coup d'État de 1977 au Bénin, ou Opération Crevette est la tentative ratée d'une équipe de mercenaires français de renverser le gouvernement de la République populaire du Bénin dirigé par Mathieu Kérékou dont le parti communiste, le Parti de la révolution populaire du Bénin (PRPB), était le seul parti politique autorisé dan...

Indian filmmaking in Rajasthan Indian cinema Assamese (Jollywood) Badaga Bengali (Tollywood) Bhojpuri (Bhojwood) Bihari Bodo Chhattisgarhi (Chhollywood) Deccani (Dollywood) Dogri (Pahariwood) English Gujarati (Gollywood) Haryanvi Hindi (Bollywood) Jharkhand Kashmiri Kannada (Sandalwood) Khasi Khortha Kokborok Konkani Kutchi Malayalam (Mollywood) Marathi Meitei Nagpuri Odia (Ollywood) Punjabi (Pollywood) Rajasthani Sambalpuri Sanskrit Santali (Sollywood) Sindhi Tamil (Kollywood) Telugu (Tollyw...

German mathematician Albrecht Beutelspacher (2007) Albrecht Beutelspacher (born 5 June 1950) is a German mathematician and founder of the Mathematikum. He is a professor emeritus at the University of Giessen, where he held the chair for geometry and discrete mathematics from 1988 to 2018. Biography Beutelspacher studied from 1969 to 1973 math, physics and philosophy at the University of Tübingen and received his PhD 1976 from the University of Mainz. His PhD advisor was Judita Cofman. From 1...

American actor Alfred LuntPhotograph by Carl Van Vechten in 1932BornAlfred David Lunt Jr.(1892-08-12)August 12, 1892Milwaukee, Wisconsin, U.S.DiedAugust 3, 1977(1977-08-03) (aged 84)Chicago, Illinois, U.S.Resting placeForest Home CemeteryEducationCarroll CollegeEmerson CollegeOccupationsActordirectorYears active1912–1966Spouse Lynn Fontanne (m. 1922) Alfred David Lunt (August 12, 1892 – August 3, 1977) was an American actor and director, best known...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (August 2020) (Learn how and when to remove this template message)This biography of a living person needs additional citations for verification. Please help by ...

Canadian non-profit promoting social and environmental sustainability among young people This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's notability guidelines for companies and organizations. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significan...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Real Stories – news · newspapers · books · scholar · JSTOR (July 2008) (Learn how and when to remove this template message) Australian TV series or program Real StoriesReal Stories title screenCreated byHamish BlakeAndy LeePresented byJennifer AdamsStarringHamish BlakeAndy ...

Church in Wiener Neustadt, AustriaSt. George's Cathedral, Wiener NeustadtCathedral of the Austrian Military OrdinariateKathedrale St. GeorgLocationWiener NeustadtCountry AustriaDenominationRoman Catholic Church Interior view St. George's Cathedral in Wiener Neustadt[1] (German: Kathedrale St. Georg) is the cathedral of the Military Ordinariate of Austria and a minor basilica. It is located inside the castle, Burg Wiener Neustadt.[2] The church, begun in 1440 on the west s...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Miami International Mall – news · newspapers · books · scholar · JSTOR (February 2018) (Learn how and when to remove this template message) Shopping mall in Florida, United StatesMiami International MallEast entrance between JCPenney and Kohl'sLocationDoral, Fl...

Motor vehicle Maserati Tipo 26OverviewManufacturerMaseratiProduction1926-1932[1]AssemblyBologna, ItalyDesignerAlfieri MaseratiBody and chassisClassRace carLayoutFR layoutRelatedMaserati Tipo 26BPowertrainEngine1.5 L s/c I8Transmission3-speed manual (4-speed since 1927)[2]DimensionsWheelbase2,650 mm (104 in) (2,580 mm (102 in) since 1928)[2]Curb weight720-780 kgChronologySuccessorMaserati 4CM The Maserati Tipo 26 was a model of Grand Prix r...