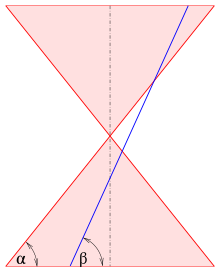
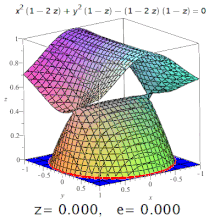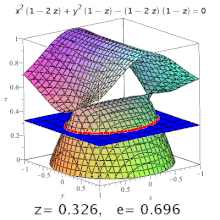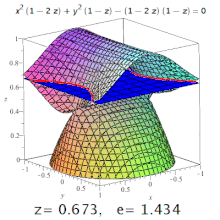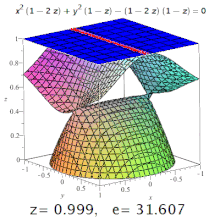
Eccentricity (mathematics)
|
Read other articles:

此條目需要擴充。 (2015年10月23日)请協助改善这篇條目,更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 此條目需要补充更多来源。 (2015年10月23日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:星際大戰:複製人之戰 (2008年電視影集) — 网页、

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Bupati SamosirLambang Kabupaten SamosirPetahanaVandiko Timotius Gultomsejak 26 April 2021Masa jabatan5 tahunDibentuk7 Januari 2004; 19 tahun lalu (2004-01-07)Pejabat pertamaMangindar SimbolonWakilMartua SitanggangSitus websamosirkab.go.id Berikut ini adalah Daftar Bupati Kabupaten Samosir: No Foto Nama Mulai Jabatan Akhir Jabatan Wakil Bupati Keterangan — Wilmar Eliaser Simanjorang 15 Januari 2004[1] 13 September 2005[1] Penjabat 1. Mangindar Simbolon 13 September ...

Baron Philippe de Rothschild (1935) Baron Georges Philippe de Rothschild (* 13. April 1902 in Paris; † 20. Januar 1988 ebenda) war ein französischer Unternehmer, Automobilrennfahrer und Eigentümer des Weingutes Château Mouton-Rothschild in Pauillac bei Bordeaux. Er war der Ur-Enkel von Baron Nathaniel de Rothschild, der 1853 das Weingut als Château Brane Mouton erworben und in „Château Mouton-Rothschild“ umbenannt hatte.[1] Philippe de Rothschild machte aus Mouton-Rothschil...

Galaxy in the constellation Coma Berenices NGC 4860Eliptical galaxy NGC 4860 (center) and spiral galaxy NGC 4858 (left).Observation data (J2000 epoch)ConstellationComa BerenicesRight ascension12h 59m 03.91s[1]Declination+28° 07′ 25.3″[1]Redshift0.02645[1]Heliocentric radial velocity7825 km/s[1]Distance360 Mly (110 Mpc)Group or clusterComa ClusterApparent magnitude (V)13.5Apparent magnitude (B)14.5CharacteristicsTyp...

American judge (born 1974) Nancy AbuduJudge of the United States Court of Appeals for the Eleventh CircuitIncumbentAssumed office May 26, 2023Appointed byJoe BidenPreceded byBeverly B. Martin Personal detailsBornNancy Gbana Abudu1974 (age 48–49)Alexandria, Virginia, U.S.EducationColumbia University (BA)Tulane University (JD) Nancy Gbana Abudu (born 1974)[1] is an American lawyer from Georgia who serves as a United States circuit judge of the United States Court of Appea...

On the SpotGenreMusik (2008-2011)Majalah berita dan gaya hidup (2009-sekarang)PengembangTrans Corp(1 September 2008-14 Desember 2013)Trans Media (15 Desember 2013-sekarang)Pengisi suaraAnanda Omesh (2008)Ruben Onsu dan Thalita Latief (2008-2009)Aditya Viraswari/Agni Nda Batubara/Pinky Andriyani Kardi (2009–sekarang)Lagu pembukaChinese Fairytale - Tiger BabyLagu penutupBervariasiNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim16Jmlh. episode5.551 (berjalan pada 12 Nopember 2023)Ril...

1978 single by Momoe YamaguchiPlayback Part 2Single by Momoe Yamaguchifrom the album Dramatic LanguageJapaneseB-sideKakeReleasedMay 1, 1978 (1978-05-01)Recorded1978GenreKayōkyokuLength3:20LabelCBS SonyComposer(s)Ryudo UzakiLyricist(s)Yoko AkiProducer(s)Masatoshi SakaiMomoe Yamaguchi singles chronology Otomegi Kyō (1978) Playback Part 2 (1978) Zettai Zetsumei (1978) Playback Part 2 (プレイバックPart2, Pureibakku Pāto Tsū) is the 22nd single by Japanese idol Momoe Yamag...

Japanese visual novel Like LifeLike Life Renewal Edition visual novel cover.ライク・ライフ(Raiku Raifu)GenreDrama, Harem GameDeveloperHooksoftPublisherHooksoft (Windows)GN Software (PS2/PSP)NTT DoCoMo (FOMA)GenreEroge, Visual novelPlatformWindows, PS2, FOMA, PSPReleasedMay 28, 2004 (Windows)April 28, 2005 (PS2) August 24, 2006 (PS2 re-release)August 17, 2007 (FOMA) September 28, 2007 (PC Renewal) October 1, 2009 (PSP) Light novelWritten byJōji KamioIllustrated byHirokō Buda...

Iranian Shi'a jurist and political activist (1839–1911) Grand Ayatullah SheikhMuhammad Kazim Khurasaniمحمدکاظم خراسانیPersonalBorn1839 (1839)Mashhad, IranDied12 December 1911(1911-12-12) (aged 71–72)Najaf, IraqResting placeImam Ali ShrineReligionIslamNationalityIranianParentMulla Husayn Herati (father)RegionNajaf, IraqJurisprudenceTwelver Shia IslamNotable work(s)Kefayat al-UsulKnown for1. Developing modern Shi'ite Usul al-Fiqh 2. Leading the first democratic...

Gapan component city (en) Tempat Negara berdaulatFilipinaRegion of the Philippines (en) Luzon TengahProvinsi di FilipinaNueva Ecija NegaraFilipina PendudukTotal122.968 (2020 )Tempat tinggal30.186 (2020 )Bahasa resmiBahasa Kapampangan, Tagalog dan Bahasa Iloko GeografiLuas wilayah118 km² [convert: unit tak dikenal]Ketinggian41 m Berbatasan denganSan Leonardo SejarahPembuatan1732 Informasi tambahanKode pos3105 Zona waktuUTC+8 Kode telepon44 Lain-lainSitus webLaman resmi Data s...

Zamek w Oświęcimiu nr rej. AK-11/Bi/23/Kr/934 z 30.04.1934, A-390 z 17.11.1972, A-279/78 z 27.02.1978 Zamek w Oświęcimiu Państwo Polska Województwo małopolskie Miejscowość Oświęcim Położenie na mapie województwa małopolskiegoZamek w Oświęcimiu Położenie na mapie PolskiZamek w Oświęcimiu 50°03′28,0080″N 19°17′46,7520″E/50,057780 19,296320 Multimedia w Wikimedia Commons Strona internetowa Zamek w Oświęcimiu – budowla wzniesiona w średnio...

Australian industrial relations law Parliament of Australia Long title An Act relating to workplace relations, and for related purposes CitationNo. 28, 2009 or No. 28, 2009 as amendedTerritorial extentStates and territories of AustraliaEnacted byHouse of RepresentativesRoyal assent7 April 2009Commenced1 July 2009Legislative historyIntroduced byRudd governmentFirst reading25 November 2008Second reading1 December 2008First reading5 December 2008Second reading11 March 2009Related legislatio...

The Last Days of PompeiiPoster rilis teatrikalSutradara Ernest B. Schoedsack Merian C. Cooper Produser Merian C. Cooper Ditulis olehRuth Rose[1]CeritaJames Ashmore Creelman[1]BerdasarkanThe Last Days of Pompeiikarya Edward Bulwer-LyttonPemeranPreston FosterAlan HaleBasil RathboneJohn WoodDavid HoltDorothy WilsonPenata musikRoy WebbSinematograferJ. Roy HuntJack Cardiff (tak disebutkan)PenyuntingArchie MarshekPerusahaanproduksiRKO Radio PicturesDistributorRKO Radio Picture...

American actress and model Cynthia GibbGibb at SBIFF 2023BornCynthia Lowrie Gibb (1963-12-14) December 14, 1963 (age 59)Bennington, Vermont, U.S.EducationStaples High SchoolOccupationsActressmodelYears active1980–presentKnown forFameGypsyYoungbloodShort Circuit 2Holiday AffairThe Karen Carpenter StorySpouseScott Kramer (divorced)Children3Websitecynthiagibb.me Cynthia Gibb (born December 14, 1963) is an American actress and former model who has starred in film and on televisio...

Indonesian TV series or program It's Showtime IndonesiaGenreVariety show, comedy talent showCreated byABS-CBN CorporationBased onIt's ShowtimePresented by Raffi Ahmad Luna Maya Chika Jessica Indra Herlambang Leo Consul JudgesVariousOpening themeShowtime performed by It's Showtime hostsCountry of originIndonesiaOriginal languageIndonesianProductionProduction locationsStudio 10MNC Studios Jakarta, IndonesiaRunning time90 minutesProduction companyMNC Productions EntertainmentOriginal releas...

Red Army manкрасноармеецCountry Soviet UnionService branchRed ArmyFormation1918AbolishedJuly 1946Next higher rank Section commander (1935–1940) Yefreytor (1940–1946) Equivalent ranksRed Fleet man Red Army man (Russian: Красноармеец, romanized: Krasnoarmeyets) was the lowest military rank in the Red Army of the Soviet Union from 1918 to 1946.[1] On 30 November 1917, after the October Revolution, the Military Revolutionary Committee cancelled all of...

Election in Pennsylvania Main article: 1900 United States presidential election 1900 United States presidential election in Pennsylvania ← 1896 November 6, 1900 1904 → Nominee William McKinley William Jennings Bryan Party Republican Democratic Home state Ohio Nebraska Running mate Theodore Roosevelt Adlai Stevenson I Electoral vote 32 0 Popular vote 712,665 424,232 Percentage 60.74% 36.16% County Results McKinley 40-50% ...

Approximate area of the South West Wilderness of Tasmania The South West Wilderness of Tasmania, Australia is a remote and inaccessible region of South West Tasmania containing unspoilt scenery, rugged peaks, wild rivers, unique flora and fauna, and a long and rugged coastline. Parts of the wilderness are more than 50 km from the nearest road, so the only access to the area is by foot, air or sea. It has been known by a variety of names over the last century, and the label has been affec...

1959 Pakistani film KoelDirected byMasood ParvezWritten byShams LakhnaviProduced bySaifuddin SaifStarring Noor Jehan Neelo Aslam Pervaiz Allauddin Edited byHasnain RizviMusic byKhwaja Khurshid AnwarRelease date1959CountryPakistanLanguageUrdu Koel is a Pakistani 1959 musical romantic drama film directed by Masood Parvez. The film stars Noor Jehan with Aslam Pervaiz, Neelo and Allauddin in supporting roles.[1][2] This film is regarded as one of the best musical films of Lollywoo...