Rose (mathematics)
|
Read other articles:

Запрос «Гадкие лебеди» перенаправляется сюда; см. также другие значения. Гадкие лебеди Обложка неавторизованного издания 1972 года (художник Николай Николенко)[1] Жанр повесть, научная фантастика Автор братья Стругацкие Язык оригинала русский Дата написания 5 октя

Muscle connectingthe epicranial aponeurosis to the helix of the ear Anterior auricular muscleFace and neck muscles. Anterior auricular muscle shown in red.The muscles of the auricula. Anterior auricular is at right (indicated by the red arrow).DetailsOrigintemporal fasciaInsertionmajor helix (ear)Arteryposterior auricular arteryNervetemporal branch of facial nerveActionspulls ear forwardIdentifiersLatinMusculus auricularis anteriorTA98A04.1.03.020TA22089FMA46856Anatomical terms of muscle[...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2020) سيف الله أعظم (بالبنغالية: সাইফুল আজম) معلومات شخصية الميلاد سنة 1941 مقاطعة بابنا الوفاة 14 يونيو 2020 (78–79 سنة)[1] دكا[2] مواطنة ا�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2018) ألبرت كرايغ معلومات شخصية الميلاد 3 يناير 1962 (61 سنة) غلاسكو مركز اللعب وسط الجنسية المملكة المتحدة المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1981–1986 دمب�...

Gospel Music AssociationGMA LogoAbbreviationGMAFormation1964AffiliationsGMA FoundationWebsitewww.gospelmusic.org The Gospel Music Association (GMA) is a nonprofit organization founded in 1964 for the purpose of supporting and promoting the development of all forms of gospel music.[1] As of 2011, there are about 4,000 members worldwide.[2] The GMA's membership comprises a network of artists, industry leaders, retail stores, radio stations, concert promoters and local churches i...

Kit Mikayi, un conocido tor cerca de Kisumu, Kenia. Tor. Un tor en geomorfología es un relieve residual que se produce por afloramientos de materiales de mayor dureza como por ejemplo el granito. Cuando se produce la meteorización, estos materiales tienen mayor resistencia que los de su alrededor, de modo que no sufren desplazamiento, generalmente teniendo morfología de colinas. Un tor aparece normalmente como un montón de losas de roca o como una serie de planchas en posición vertical, ...
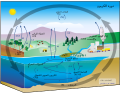
اقتصاد بيئيصنف فرعي من اقتصاد الموضوع بيئة طبيعية تعديل - تعديل مصدري - تعديل ويكي بيانات جزء من سلسلة مقالات حولاقتصاد تاريخأفرع تاريخ الاقتصاد مدارس الاقتصاد اقتصاد سائد اقتصاد بدعي المنهجية الاقتصادية اقتصاد سياسي الاقتصاد الجزئي الاقتصاد الكلي اقتصاد دولي اقتصاد تطبي

1938 EuropeanAthletics ChampionshipsTrack events100 mmenwomen200 mmenwomen400 mmen800 mmen1500 mmen5000 mmen10,000 mmen80 m hurdleswomen110 m hurdlesmen400 m hurdlesmen3000 msteeplechasemen4×100 m relaymenwomen4×400 m relaymenRoad eventsMarathonmen50 km walkmenField eventsHigh jumpmenwomenPole vaultmenLong jumpmenwomenTriple jumpmenShot putmenwomenDiscus throwmenwomenHammer throwmenJavelin throwmenwomenCombined eventsDecathlonmenvte The men's 1500 metres at the 1938 European Athletics Champ...

七宗町立上麻生中学校 北緯35度32分14.0秒 東経137度06分56.7秒 / 北緯35.537222度 東経137.115750度 / 35.537222; 137.115750座標: 北緯35度32分14.0秒 東経137度06分56.7秒 / 北緯35.537222度 東経137.115750度 / 35.537222; 137.115750国公私立の別 公立学校設置者 七宗町設立年月日 1947年共学・別学 男女共学学校コード C121250400023 所在地 〒509-0402 岐阜県加茂郡七宗町川�...

Japanese professional wrestler (born 1995) El LindamanEl Lindaman in January 2022Birth nameYuga Hayashi (林悠河, Hayashi Yūga)Born (1995-02-12) February 12, 1995 (age 28)[1]Nakano, Tokyo, Japan[1]Professional wrestling careerRing name(s)El Lindaman[2]Yuga Hayashi[2]Billed height1.61 m (5 ft 3 in)[1]Billed weight70 kg (154 lb)[1]Trained byDragon Gate DojoDebutApril 4, 2014[1] Yuga Hayashi (林悠河, Haya...

For other uses, see Get Rich or Die Tryin' (disambiguation). 2003 studio album by 50 CentGet Rich or Die Tryin'Studio album by 50 CentReleasedFebruary 6, 2003[1]Genre East Coast hip hop gangsta rap Length53:44Label Interscope Shady Aftermath G-Unit ProducerDr. Dre (exec.)Eminem (also exec.)Sha Money XL (also exec.)50 Cent (exec.)Sean BlazeDarrell BranchDirty SwiftDJ RadTerence DudleyMike ElizondoJohn J-Praize FreemanMegahertzMr. PorterRed SpydaReefRockwilder50 Cent chronology ...

Government engineering college in Arwal, Bihar This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Government Engineering College, Arwal – news · newspapers · books · scholar · JSTOR (February 2020) (Learn how and when to remove this template message) Government Engineering College, ArwalTypeGovernment Engineeri...

Book used to teach reading to children This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Basal reader – news · newspapers · books · scholar · JSTOR (June 2023) (Learn how and when to remove this template message) Reading book redirects here. For other uses, see Reading book (disambiguation). Part of a series o...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Oxfam Glamour Models – news · newspapers · books · scholar · JSTOR (July 2009) (Learn how and when to remove this template message) Oxfam Glamour ModelsBackground informationOriginMiddlesbrough, EnglandGenresNoise rock, indie rock, post-punkYears active2005...

Grade II listed building in London, England Metro Central Heights Metro Central Heights is a group of residential buildings in Walworth in the London Borough of Southwark. It was originally known as Alexander Fleming House, a multi-storey office complex designed by Hungarian-born modernist architect Ernő Goldfinger and constructed in the early 1960s for Arnold Lee of Imry Properties. The design was favoured both by the property developer Imry and by the London County Council as it promised t...

1992 book on linguistics by Anthony Burgess A Mouthful of Air First edition (UK)AuthorAnthony BurgessLanguageEnglishSubjectLinguisticsPublisherHutchinson (UK)William Morrow & Co (US)Publication dateOctober 1992 (UK)August 1993 (US)Media typeHardcoverPages352ISBN0-09-177415-2OCLC27224188Dewey Decimal420 20LC ClassPE1072 .B796 1992 A Mouthful of Air: Language and Languages, Especially English is a book on linguistics by Anthony Burgess published in 1992.[1][2] Topi...

Railway station in Pakistan Rajar Railway Station راجر ریلوے اسٹیشن راڄڙ ريلوي اسٽيشنGeneral informationOwned byMinistry of RailwaysLine(s)Mirpur Khas–Nawabshah RailwayOther informationStation codeRJHServices Preceding station Pakistan Railways Following station Sinjhorotowards Mirpur Khas Mirpur Khas–Nawabshah Railway(defunct) Khadrotowards Nawabshah Rajar Railway Station (Urdu: راجر ریلوے اسٹیشن, Sindhi: راڄڙ ريلوي اسٽيشن) is l...

Binny Golf ClubBinny Golf ClubClub informationLocationBroxburn, West Lothian, ScotlandEstablished2002TypePublicTotal holes9WebsiteBinny Golf ClubPar35Length2458 yards Binny Golf Club is a golf course located in Broxburn, West Lothian, Scotland.[1] History Binny Golf Club was formed in April 2002 two years after the opening by Bernard Gallacher, of Oatridge Golf Course, which lies in the grounds of Binny Estate adjacent to East Binny House. The name Binnie is thought to come from a loc...

Open-source software for adding notes to PDF files XournalStable release0.4.8.2016 (July 20, 2017) Repositorysourceforge.net/p/xournal/code/ci/master/tree/ Written inC, C++Operating systemLinux, Unix-like, macOS, WindowsLicenseGPL v2WebsiteXournal++ github.com/xournalpp/xournalpp Xournal is an open source tool for annotating PDF files. It supports pen, mouse, and keyboard input.[1] It and the related Xournal++ are commonly used for adding annotations and electronic signatures to PDF f...

Tatak han Rehiyon han Lombardiya Bandera han Lombardiya Mapa kun diin makikit-an an mga lalawigan han Rehiyon han Lombardiya An Lombardiya (Initalyano: Lombardia [lombarˈdiːa]; Linumbardo: Lombardia, Katundan nga Linombardo: [lũbarˈdiːa], o kundi man Lombardéa, Sinirangan nga Linombardo: [lombarˈde.a]; ha Kinatsila: Lombardía; ha Iningles: Lombardy /ˈlɒmbərdi, ˈlʌm-/ LOM-bər-dee-,_-LUM[1][2]) amo an usa (1) ha karuhaan (20) ka rehiyon han Italya. An...



















![{\displaystyle {\begin{aligned}{\frac {1}{2}}\int _{0}^{2\pi }(a\cos(k\theta ))^{2}\,d\theta &={\frac {a^{2}}{2}}\left(\pi +{\frac {\sin(4k\pi )}{4k}}\right)={\frac {\pi a^{2}}{2}}&&\quad {\text{for even }}k\\[8px]{\frac {1}{2}}\int _{0}^{\pi }(a\cos(k\theta ))^{2}\,d\theta &={\frac {a^{2}}{2}}\left({\frac {\pi }{2}}+{\frac {\sin(2k\pi )}{4k}}\right)={\frac {\pi a^{2}}{4}}&&\quad {\text{for odd }}k\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58ed28979bb8ca9b9a7b7f44593149ea14500e9d)




