Stabilitätstheorie
|
Read other articles:

Опис Обкладинка альбому Дженіс Джоплін I Got Dem Ol' Kozmic Blues Again Mama! (1969) Джерело [1] Час створення 1969 Автор зображення невідомо Ліцензія Це зображення є обкладинкою музичного альбому або синглу. Найімовірніше, авторськими правами на обкладинку володіє видавець альбому (синглу) �...
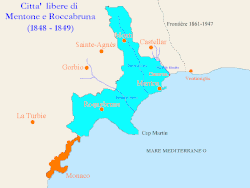
У Вікіпедії є статті про інші значення цього терміна: Грімальді (значення). Територія князівства Монако у 1848—1849 рр. Гримальдійська культура — археологічна культура пізнього палеоліту. Отримала назву за місцем знахідки — «печерами Грімальді» (біля міста Мантон �...

Big Fish: A Novel of Mythic Proportions PengarangDaniel WallaceNegaraAmerika SerikatBahasaInggrisPenerbitPandher BooksTanggal terbit1 Oktober 1998Halaman180 halamanISBNISBN 1-56512-217-8 Big Fish: A Novel of Mythic Proportions adalah sebuah novel karya Daniel Wallace yang dirilis pada tanggal 1 Oktober 1998. Novel ini bercerita tentang Edward Bloom, seorang pria yang selalu bercerita bahwa ia telah melakukan banyak petualangan menakjubkan, bertemu dengan orang-orang dan mengunjungi tempa...

Amanah Wali 5Genre Drama Religi Komedi PembuatMNC PicturesCeritaMelvi YendraLovely NadaHenny SuryaSutradara Kiky Zkr Bobby Herlambang Indrawan Yogi Yose Pemeran Apoy Faank Ovie Tomy Rano Karno Alfie Alfandy Teddy Syach Erick Estrada Salshabilla Adriani Malida Dinda Zacky Zimah Tarsan Hj. Tonah Rizky Inggar Della Puspita Sintya Marisca Valeria Stahl Marsha Risdasari Nahza Soebijakto Teddy Oktora Roby Tremonti Dedi Ilyas Buyung Malelo Mono Cocok Bombom Aldo Aminudin Maryati Tohir Herry Ujang Su...

Hüpstedt Stadt und Landgemeinde Dingelstädt Koordinaten: 51° 20′ N, 10° 27′ O51.32611111111110.443055555556453Koordinaten: 51° 19′ 34″ N, 10° 26′ 35″ O Höhe: 453 m ü. NN Einwohner: 1550 (2009) Eingemeindung: 1. Januar 1994 Eingemeindet nach: Dünwald Postleitzahl: 37351 Vorwahl: 036076 Blick über den OrtBlick über den Ort Hüpstedt ist ein Dorf im Obereichsfeld und zugleich Ortsteil der Stadt und ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Kiri: Plasmid pGLO dibawah cahaya normal Kanan: Plasmid pGLO divisualisasi dibawah sinar UV Plasmid pGLO merupakan plasmid modifikasi yang telah disisipkan gen GFP yang berasal dari ubur-ubur Aequorea victoria.[1] Plasmid ini memiliki ukuran 5...

克劳德·尼科里埃尔Claude Nicollier出生1944年9月2日瑞士沃韦国籍 瑞士航天生涯瑞士宇航员在太空时间42天12小时5分钟任务STS-46、STS-61、STS-75、STS-103任务徽章退役2007年3月 克劳德·尼科里埃尔(Claude Nicollier,1944年9月2日—)是瑞士到目前为止唯一的一名宇航员,曾经进行过四次太空飞行[1][2]。 个人经历和教育 1962年在洛桑中学毕业后,他进入了洛桑大学学习物理学

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Sebuah voltage regulator linear LM7805 5V dengan 2 kapasitor dekopling Dekopling adalah penghilangan atau pengurangan isyarat AC yang tidak diinginkan di suatu titik dalam rangkaian. Isyarat AC yang tidak diinginkan itu bisa merupakan kerut pencatu day...

Басистюк-Гаптар Ольга ІванівнаНародилася 19 серпня 1950(1950-08-19) (73 роки)с. Поляни, Хмельницька областьГромадянство СРСР УкраїнаДіяльність concert singer, оперна співачкаAlma mater Львівська національна музична академія імені Миколи Лисенка (1974)Заклад Львівська обласна філар�...

American basketball player (born 1973) Theo RatliffRatliff with the Pistons in 2008Personal informationBorn (1973-04-17) April 17, 1973 (age 50)Demopolis, Alabama, U.S.NationalityAmericanListed height6 ft 10 in (2.08 m)Listed weight235 lb (107 kg)Career informationHigh schoolDemopolis (Demopolis, Alabama)CollegeWyoming (1991–1995)NBA draft1995: 1st round, 18th overall pickSelected by the Detroit PistonsPlaying career1995–2011PositionCenter / power forwardNumb...

A view of rock carvings on rock shelter Right Swastika An engraving of dancing woman Petroglyph of Unicorn Rider The Ancient Rock Carvings of Sindh have been explored in Kirthar Mountains Range, Sindh, Pakistan. The Kirthar Mountains Range covers a distance of 190 miles (300 Kilometers)[1] in boundaries of Jacobabad District, Qambar Shahdadkot District, Dadu District and Jamshoro District from north to south up to Karachi, Sindh. Rock carving sites The numerous sites of ancient rock c...

Taman Bunga aiNusantara Taman Bunga Nusantara adalah sebuah taman bunga seluas 35 hektare yang terletak dekat Gunung Gede Pangrango dan Kebun Teh Bogor dengan jarak tempuh sekitar 2,5 - 3 jam perjalanan dari Jakarta, tepatnya berada di antara dua desa yaitu, Kawungluwuk, Sukaresmi, Cianjur dengan Sukawangi, Sukamakmur, Jonggol. Di taman ini disimpan berbagai tipe bunga dari seluruh dunia yang tumbuh di tempat ini, dalam hal ini terutama budi daya anggrek. Diperkirakan ada sekitar 2000 jenis a...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (نوفمبر 2019) أ. إلمر كرويل معلومات شخصية تاريخ الميلاد 5 ديسمبر 1862 تاريخ الوفاة 1 يناير 1952 (89 سنة) مواطنة الولايات المتحدة الحياة العملية المهنة نقاش خشب [�...

American fashion designer Tracy ReeseBorn (1964-02-12) February 12, 1964 (age 59)Detroit, MichiganNationalityAmericanEducationParsons School of DesignLabels Tracy Reese Plenty Frock! Tracy Reese Black Label Tracy Reese designs, 2008. Regina King in Tracy Reese (2010) Tracy Reese (born February 12, 1964) is an American fashion designer who specializes in women's ready-to-wear clothing, accessories, and home fashions such as linens. She is a board member of the Council of Fashion Designers...

Australian rules footballer (1947–2020) Australian rules footballer Michael Bowden Bowden playing for Richmond in the VFLPersonal informationFull name Michael John BowdenDate of birth (1947-03-21)21 March 1947Date of death 11 April 2020(2020-04-11) (aged 73)Original team(s) St Kevin's CollegeHeight 185 cm (6 ft 1 in)Weight 94 kg (207 lb)Position(s) Ruck-roverPlaying career1Years Club Games (Goals)1967–1971 Richmond 59 (20) 1 Playing statistics correct to...

House in Oshawa, Ontario 43°54′16″N 78°52′5″W / 43.90444°N 78.86806°W / 43.90444; -78.86806 ParkwoodView toward the front of the house in 2007Location270 Simcoe Street NorthOshawa, Ontario, CanadaL1G 4T5Original useResidential estateCurrent useHistoric house museumWebsiteparkwoodestate.com National Historic Site of CanadaDesignated1989 The Parkwood Estate, located in Oshawa, Ontario, was the residence of Samuel McLaughlin (founder of General Motors of Canad...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Francisco P. Felix Memorial National High School – news · newspapers · books · scholar · JSTOR (August 2023) (Learn how and when to remove this template message) Public school in Cainta, Rizal, PhilippinesFrancisco P. Felix Memorial National High SchoolPang-ala...

Государство-сателлит ФранцииАнконитанская республикаRepubblica Anconitana Флаг ← → 19 ноября 1797 — 7 марта 1798 Столица Анкона Язык(и) Итальянский язык Официальный язык итальянский Форма правления Республика Анконитанская республика (итал. Repubblica Anconitana) — дочерняя ре�...
American TV series or program These Are the DaysVoices ofFrank CadyPamelyn FerdinMoosie DrierSam EdwardsJack HaleyHenry JonesJune LockhartAndrew ParksCountry of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes16ProductionExecutive producersWilliam HannaJoseph BarberaRunning time30 minutesProduction companyHanna-Barbera ProductionsOriginal releaseNetworkABCReleaseSeptember 7, 1974 (1974-09-07) –September 27, 1975 (1975-09-27) These Are the Days is...

Istirja dalam aksara Arab. Inna lillahi wa inna ilaihi raji'un (Arab: إِنَّا لِلَّٰهِ وَإِنَّا إِلَيْهِ رَاجِعُونَ, ʾinnā li-llāhi wa-ʾinna ʾilayhi rājiʿūna) atau Istirja adalah potongan dari ayat Al-Qur'an, dari Surah Al-Baqarah, ayat 156. Arti dari frasa tersebut adalah Sesungguhnya kita ini adalah milik Allah, dan kepada-Nya lah kita akan kembali. Istirja umum diucapkan oleh Muslim ketika mendapatkan musibah. Signifikansi Dalam Islam,...





























