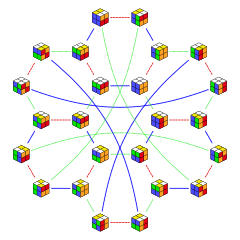
Nauru graph
| |||||||||||||||||||||||||||||
Read other articles:

Yuki FukushimaInformasi pribadiKebangsaan JepangLahir6 Mei 1993 (umur 30)Prefektur Kumamoto, JepangTinggi164 cm (5 ft 5 in)Ganda PutriPeringkat tertinggi1 (21 Juni 2018)Peringkat saat ini8 bersama Sayaka Hirota (8 November 2022[1])Profil di BWFTerakhir diperbarui: 9 Desember 2021 Ini adalah nama Jepang, nama keluarganya adalah Fukushima. Yuki Fukushima (福島由紀code: ja is deprecated , Fukushima Yuki, lahir 6 Mei 1993) adalah pemain bulu tangkis ...

Type of head cover This article is about the headgear. For other uses, see Chaperon (disambiguation). Cappuccio redirects here. For other uses, see Cappuccio (disambiguation). Probable self-portrait by Jan van Eyck, 1433. The chaperon is worn in style A with just a patch of the bourrelet showing (right of centre) through the cornette wound round it (practical for painting in).[1] A chaperon (/ˈʃæpəroʊn/ or /ˈʃæpərɒn/; Middle French: chaperon) was a form of hood or, later, hi...

Запрос «НЭП» перенаправляется сюда; см. также другие значения. РСДРП — РСДРП(б) — РКП(б) —ВКП(б) — КПССИстория партии Октябрьская революция (1917) Военный коммунизм (1918—1921) Новая экономическая политика (1921—1928) Ленинский призыв (1924) Внутрипартийная борьба (1926—1933) Сталиниз...

Ne pas confondre avec Carolina Reiber, athlète suisse. Carolin ReiberCarolin Reiber en 2014BiographieNaissance 2 novembre 1940 (83 ans)MunichNationalité allemandeActivité Animatrice de télévisionPère Ludwig ReiberAutres informationsA travaillé pour ZDFDistinctions Prix de la télévision bavaroise (2020)Ordre bavarois du Méritemodifier - modifier le code - modifier Wikidata Carolin Reiber (né le 2 novembre 1940 à Munich) est une animatrice de télévision allemande. Biographie ...

Classification of lumber commodities Black spruce stand at Arctic Chalet, Inuvik, NT Spruce-pine-fir (SPF) is a classification of lumber that can be traded on commodities exchanges. In Canada, and parts of the United States, most of the spruce tree species, pine tree species, and fir tree species share similar physical and mechanical characteristics, to the point where lumber derived from any of these species are interchangeable for construction purposes. Therefore, it makes sense to harvest ...

Kristus dan Buddha oleh Paul Ranson, 1880 Meskipun berbagai persamaan telah ditarik antara agama Buddha dan Kekristenan, ada perbedaan antara kedua agama ini yang dimulai dengan posisi monoteisme inti dari Kekristenan, dan orientasi agama Buddha ke arah nonteisme (kurangnya relevansi keberadaan sang dewa pencipta) yang bertentangan dengan ajaran-ajaran tentang Tuhan dalam Kekristenan; dan meluas kepada pentingnya kasih karunia dalam Kekristenan berlawanan dengan penolakan campur tangan karma ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) 15 يوليو 1945. ناجون من معسكر بوخنفالد يصلون إلى حيفا وقبض عليهم البريطانيون فيما بعد.كانت هذه المقالة جزء م�...

Diagramas de Young mostrando el número de particiones de los enteros del 1 al 8. Se asignan diferentes colores a cada entero. Por ejemplo, en verde, observamos que hay 5 particiones de 4. En matemáticas discretas, una partición de un entero positivo n es una forma de descomponer n como suma de enteros positivos. Dos sumas se considerarán iguales si solo difieren en el orden de los sumandos. De modo más riguroso, una partición de un número entero positivo n es una secuencia de enteros p...

American judge (born 1949) Thomas L. AmbroSenior Judge of the United States Court of Appeals for the Third CircuitIncumbentAssumed office February 6, 2023Judge of the United States Court of Appeals for the Third CircuitIn officeFebruary 16, 2000 – February 6, 2023Appointed byBill ClintonPreceded byWalter King StapletonSucceeded byTamika Montgomery-Reeves Personal detailsBornThomas Lee Ambro[1] (1949-12-27) December 27, 1949 (age 73)Cambridge, Ohio, U.S.EducationGeo...

2010 New Zealand filmMatarikiNew Zealand theatrical release posterDirected byMichael BennettScreenplay byMichael BennettGavin StrawhanStory byIaheto Ah HiProduced byFiona CoplandStarringSara WisemanAlix BushnellSusana TangJason WuCinematographyAlun BollingerEdited byJohn GilbertMusic byDon McGlashanProductioncompanyFilmworkDistributed byArkles EntertainmentRelease dates 11 September 2010 (2010-09-11) (TIFF World Premiere) 18 November 2010 (2010-11-18) (Ne...

New Zealand footballer (born 1989) Abby Erceg Erceg with Racing Louisville FC in 2023Personal informationFull name Abby May Erceg[1]Date of birth (1989-11-20) 20 November 1989 (age 34)[1]Place of birth Whangārei, New Zealand[2]Height 1.77 m (5 ft 10 in)[1]Position(s) DefenderTeam informationCurrent team Racing LouisvilleNumber 20Youth career0000–2004 Three Kings UnitedSenior career*Years Team Apps (Gls)2004–2006 Three Kings United 36 (1...

Israeli whistleblower and journalist Anat Kam (2008) Anat Kamm (alternative spelled Anat Kam, Hebrew: ענת קם; born in 1987 in Jerusalem) is an Israeli journalist and former whistleblower known for her role in the Anat Kamm–Uri Blau affair. Life Born in Jerusalem in 1987,[1] Kamm attended Hebrew University Secondary School. She became interested in journalism in her youth, writing for the local newspaper Jerusalem (formerly Yedioth Jerusalem), as well as for the youth channel of...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) خلال الفترة ما بين 1920 و1946 كانت كل من سوريا ولبنان تحت الانتداب الفرنسي، الذي أقر بموجب المادة الثانية وال...

This article is about the district. For its eponymous headquarters, see Moga, Punjab. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Moga district – news · newspapers ...

Rifle cartridge .338 Winchester Magnum.375 H&H Magnum (Left) .338 Winchester Magnum (Right) US Quarter for scaleTypeRiflePlace of originUSAProduction historyManufacturerWinchester Repeating ArmsProduced1958SpecificationsParent case.375 H&H MagnumCase typeBelted, bottleneckBullet diameter.338 in (8.6 mm)Neck diameter.369 in (9.4 mm)Shoulder diameter.491 in (12.5 mm)Base diameter.513 in (13.0 mm)Rim dia...

Public school in Hawaii, United States Hilo High SchoolAddress556 Waianuenue AvenueHilo, Hawaii 96720United StatesInformationTypePublic, co-educationalMottoOnce a Viking...Always a VikingEstablished1906School districtHawaii DistrictPrincipalJasmine UrasakiFaculty84.00 (FTE)[1]Grades9-12Number of students1,272 (2020-21)[1]Student to teacher ratio15.14[1]CampusSuburbanColor(s)Blue and Gold AthleticsBig Island Interscholastic FederationMascotVikingAccreditati...

2009 massacre in Democratic Republic of Congo Makombo massacrePart of the Lord's Resistance Army insurgencyHaut-Uele District, Democratic Republic of the CongoLocationMakombo, DR CongoDate14–17 December 2009Deaths321[1]–345+250 abducted (80 children)[2]PerpetratorsLord's Resistance Army[1] Lord's ResistanceArmy insurgency Conflict history 1987–1994 1994–2002 2002–2005 Juba talks Garamba offensive Related articles War in Uganda (1986–1994) Aboke abductions A...

2002 video gameDeveloper(s)LankhorPublisher(s)MicroïdsPlatform(s)Windows PCRelease2002 Ski Park Manager is a video game released in 2002, developed by Lankhor and published by Microïds. The game has 42 challenges and three levels of difficulty. The game has a career mode, where you buy and sell your ski resorts, to acquire the most popular ones. There is a training module, to learn the techniques of the game. This is a large variety of scenarios, including bankruptcy, school holidays, snows...

2007 film SiviVCD coverDirected byK. R. Senthil NathanWritten byK. R. Senthil NathanProduced byK. SundarStarringYogiJayashree RaoAnuja IyerCinematographyP. S. SanjayEdited byG. SasikumarMusic byDharanRelease date 21 September 2007 (2007-09-21) CountryIndiaLanguageTamil Sivi is a 2007 Indian Tamil-language horror film directed by K. R. Senthil Nathan and starring Yogi, Jayashri Rao and Anuja Iyer. A remake of the 2004 Thai film Shutter, Sivi was released on 21 September 2007 acr...

American actress (1909–2003) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Karen Morley – news · newspapers · books · scholar · JSTOR (February 2021) (Learn how and when to remove this template message) Karen MorleyPromotional photograph of Morley in 1930sBornMildred Linton(1909-12-12)December 12, 1909Ot...