Movimiento armónico simple
|
Read other articles:

HidayahPoster resmiGenre Drama Religi Misteri Supernatural Horor Komedi Fiksi ilmiah PembuatMD EntertainmentBerdasarkanMajalah Hidayaholeh Variapop GroupSutradara Gul Khan & J. Ekadi Katili [a] Joko Nugroho [b] Lono Abdul Hamid & Usman Gumanti [c] Lono Abdul Hamid & Joko Nugroho [d] Gul Khan & Ferial Rachmany [i] Chep Irman Idris [j] Gul Khan [k] Sachin Kamlakar Khot & Trijaya [l] Gul Khan & Anto Agam [...

الأردن فيالألعاب الآسيوية 2002الرمزJORاللجنةاللجنة الأولمبية الأردنيةفي بوسانالميدالياتالترتيب 34 ذهبية 0 فضية 0 برونزية 2 المجموع 2 الظهور في الألعاب الآسيوية (نظرة عامة)195119541958196219661970197419781982198619901994199820022006201020142018شاركت الأردن في دورة الألعاب الآسيوية 2002 التي أقيمت في بوسان بكوري

Het graf van Jef Tinel op de Campo Santo (Gent) Jef Emiel-Jozef Tinel (Lessen, 11 mei 1885 – Gent, 25 mei 1972) was een Belgisch musicus. Hij was actief als muziekpedagoog, dirigent, organist en componist. Tinel en zijn muziek stonden ten dienste van de Kerk en de Vlaamse Beweging. Opleiding Hij was zoon van Maria Louise Vande Mergel en Emile-Oscar Tinel (1852-1913).[1] Vader was koster-organist in het Waalse Lessen in Henegouwen. Vaders jongere broer was componist Edgar Tinel (1854...

Uorodes Nacionalidade Império Sassânida Etnia Persa Ocupação Nobre Religião Zoroastrismo Uorodes (em parta: wrwd; romaniz.:Wīrōδ; em persa médio: Wīrōy; em grego clássico: Ουορωδ; romaniz.:Ouorod) foi um oficial sassânida do século III, ativo no reinado do xá Sapor I (r. 240–270). É conhecido apenas a partir da inscrição Feitos do Divino Sapor segundo a qual era mestre dos mercados (wāzārbed em persa e parta; agorânomo em grego). Aparece numa lista d...

Johannes Gropper als Kardinal Wappen von Johannes Gropper Johannes Gropper, auch Johann Gropper (* 24. Februar 1503 in Soest; † 13. März 1559 in Rom) war ein katholischer Theologe, Jurist und Kirchenpolitiker zur Zeit der Reformation. Er gilt als Verteidiger des katholischen Glaubens im Erzbistum Köln während der so genannten Kölner Reformation und als einer der bedeutendsten katholischen Theologen des 16. Jahrhunderts. Inhaltsverzeichnis 1 Leben 2 Werk 3 Literatur 4 Weblinks 5 Ein...

ConnecticutWine regionOfficial nameState of ConnecticutTypeU.S. stateYear established1788CountryUnited StatesSub-regionsSoutheastern New England AVA, Western Connecticut Highlands AVA, Eastern Connecticut Highlands AVAClimate regionContinentalTotal area5,543 square miles (14,356 km2)[1]Grapes producedAurore, Cabernet Franc, Cabernet Sauvignon, Cayuga, Chambourcin, Chardonel, Chardonnay, Frontenac, Gewurztraminer, Marechal Foch, Merlot, Pinot gris, Riesling, Seyval blanc, St. Croi...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مايو 2021) لعبت جمهورية الصين الشعبية دورًا رئيسيًا في حرب فيتنام (1955-1975). دعم الشيوعيون الصينيون منذ عام 1949 تمرد فيت مين ضد نظام الهند الصينية الفرنسية الاستعماري. وعندم...

Klemens XIIIClemens Tertius Decimus Carlo della Torre Rezzonico PapieżBiskup Rzymu Klemens XIII (1758) Kraj działania Państwo Kościelne Data i miejsce urodzenia 7 marca 1693 Wenecja Data i miejsce śmierci 2 lutego 1769 Rzym Miejsce pochówku bazylika św. Piotra Papież Okres sprawowania 6 lipca 1758–2 lutego 1769 Biskup Padwy Okres sprawowania 11 marca 1743–6 lipca 1758 Wyznanie katolicyzm Kościół rzymskokatolicki Prezbiterat 23 grudnia 1731 Nominacja biskupia 11 marca ...

Exhibition basketball game 2016 NBA All-Star Game 1234 Total West 40525351 196 East 43474637 173 DateFebruary 14, 2016ArenaAir Canada Centre and Ricoh ColiseumCityTorontoMVPRussell Westbrook (West)National anthemNelly Furtado (Canadian)Ne-Yo (American)Halftime showStingAttendance18,298NetworkTSN and Sportsnet (Canada)TNT and TBS (United States)AnnouncersMarv Albert, Reggie Miller, Chris Webber, Craig Sager, and David AldridgeKevin Harlan, Ernie Johnson, Reggie Miller, Kenny Smith, Charles Bar...

Manga by Buichi Terasawa Goku Midnight EyeGoku Midnight Eye: Part Two OVA coverMidnight Eye ゴクウ(Midnight Eye Gokū) MangaWritten byBuichi TerasawaPublished byGentoshaEnglish publisherNA: Comics One DrMasterMagazineComic BurgerDemographicSeinenOriginal run1987 – 1989Volumes3 (Japan)4 (North America) Original video animationDirected byYoshiaki KawajiriProduced byNaoko TakahashiTomiro KuriyamaWritten byBuichi TerasawaRyūzō NakanishiMusic byKazuhiko ToyamaY...

Village in Maharashtra This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Chincholi, Parner – news · newspapers · books · scholar · JSTOR (June 2023) Village in Maharashtra, IndiaChincholiVillageChincholiLocation in Maharashtra, IndiaShow map of MaharashtraChincholiChincholi (India)Show map of IndiaCo...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Shri Datta Meghe Polytechnic – news · newspapers · books · scholar · JSTOR (January 2019) (Learn how and wh...

National park in the Chubū region of Honshū, Japan Hakusan National Park白山国立公園IUCN category II (national park)HakusanLocationChūbu region, Honshū, JapanCoordinates36°09′18″N 136°47′17″E / 36.15500°N 136.78806°E / 36.15500; 136.78806Area477 km2 (184 sq mi)Established12 November 1962 Hakusan National Park (白山国立公園, Hakusan Kokuritsu Kōen) is a national park in the Chūbu region of Honshū, Japan. Established in 1962,...

Pakistani director Bilal Lashariبلال لاشاریBilal Lashari in 2014Born (1981-08-04) August 4, 1981 (age 42)[1]Lahore, Punjab, PakistanNationalityPakistaniEducationLahore University of Management Sciences, Lahore Grammar School Senior Boys Campus JTAlma materHEC Paris, Academy of Art UniversityOccupation(s)Actor, Screenwriter, CinematographerYears active2004–presentKnown forWaar, The Legend of Maula JattRelativesKamran Lashari (father)Awardssee below Bilal...

Este artigo não cita fontes confiáveis. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Agosto de 2020) Marlborough College do telhado da igreja de St Peter Marlborough College é um internato independente (particular) britânico, localizado no condado de Wiltshire na Inglaterra. Foi fundado em 1843 para educar os filhos do clero da Igreja da Ingl...

Ukrainian anarchist revolutionary (1888–1934) Bat'koNestor MakhnoНестор МахноMakhno in 1921Otaman of the MakhnovshchinaIn office30 September 1918 – 28 August 1921Preceded byPosition establishedSucceeded byViktor BilashChairman of the Military Revolutionary CouncilIn office27 July 1919 – 1 September 1919Preceded byIvan ChernoknizhnySucceeded byVolin Personal detailsBorn7 November [O.S. 26 October] 1888Huliaipole, Katerynoslav Governorate, Russian Empi...

Fernsehserie Titel Nordlicht – Mörder ohne Reue Originaltitel Den som dræber Produktionsland Dänemark, Deutschland Originalsprache Dänisch Genre Krimi, Drama Länge Originalfassung: 45 Minuten,ZDF-Fassung: 90 Minuten Episoden 12 (Originalfassung) bzw.6 (ZDF-Fassung) in 1 Staffel Produktions-unternehmen Miso Film Idee Elsebeth Egholm,Stefan Jaworski Produktion Jonas Allen,Peter Bose,Klaus Bassiner,Wolfgang Feindt,Michael Fleischer,Peter Nadermann Musik Frans Bak Erstausstrahlung 13....

Not to be confused with 9-1-1: Lone Star or with the Lone Star Series, a baseball rivalry. American TV series or program Lone StarAlso known asMidlandGenreDramaCreated byKyle KillenStarringJames Wolk Adrianne Palicki Bryce Johnson David Keith Eloise Mumford Alexandra Doke Jon Voight Mark DeklinComposerDanny LuxCountry of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes7[1]ProductionExecutive producersAmy LippmanChris KeyserKerry Kohansky RobertsKyle Kille...

صوفي من مكلنبورغ-غوسترو (بالألمانية: Sophie von Mecklenburg-Güstrow) معلومات شخصية الميلاد 4 سبتمبر 1557 فيسمار الوفاة 14 أكتوبر 1631 (74 سنة) مواطنة دوقية مكلنبورغ شفيرين الزوج فريدريك الثاني ملك الدنمارك (20 يوليو 1572–4 أبريل 1588) الأولاد آن من الدنمارككريستيان الرابع �...

IClub48GenreAcara bakatAcara varietasPembuatWishnutamaJKT48 ProjectPresenterBrandon SalimJKT48PemeranJKT48MusikAdy Julian BandNegara asal IndonesiaBahasa asliBahasa IndonesiaJmlh. musim2Jmlh. episode42ProduksiLokasi produksiStudio PSI Pengadegan (musim I)Durasi60 menit (musim I)30 menit (musim II)Rumah produksiNET. EntertainmentDentsu Inter Admark Media Group IndonesiaAKS Co., Ltd.DistributorNet Mediatama TelevisiIndika Entertainment GroupRilis asliJaringanFormat audioDolby Digital 5.1Ri...
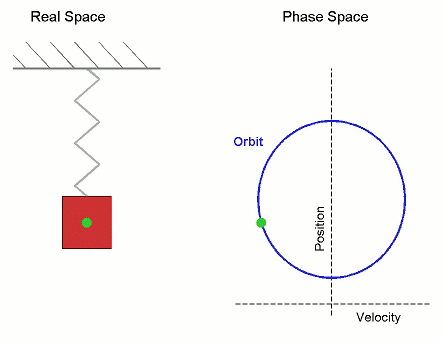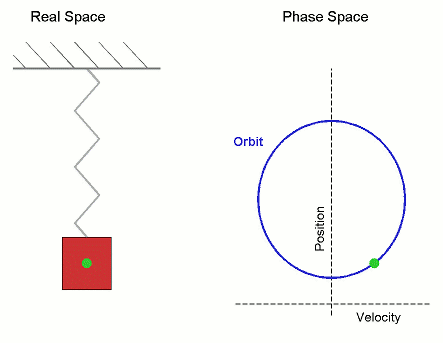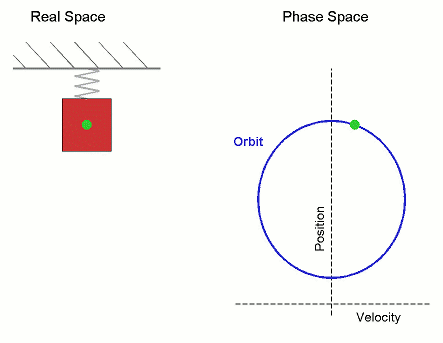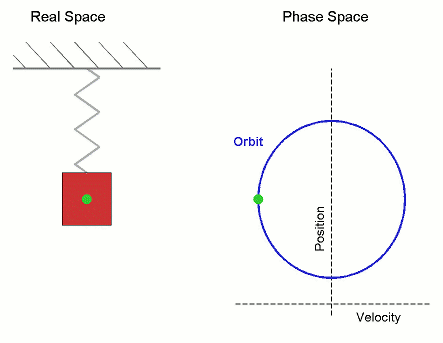

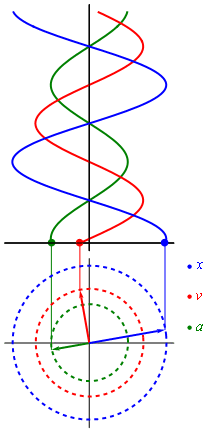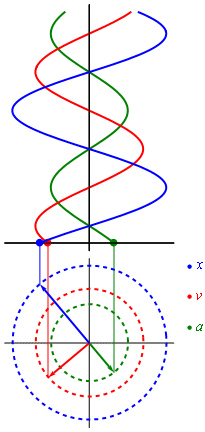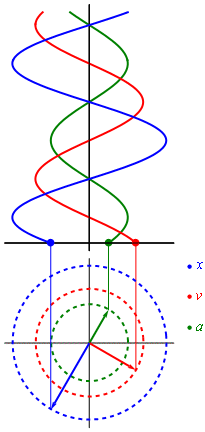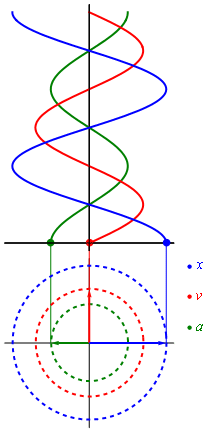









































![{\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}\left[1-\left({\frac {1}{c}}{\frac {\mathrm {d} x}{\mathrm {d} t}}\right)^{2}\right]^{-3/2}=-{\frac {k}{m}}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70612fa7c254f2a58a925471db3d1acc7d7d0f75)









