Focale
|
Read other articles:

Людмила Георгиевна Карачкина Дата рождения 3 сентября 1948(1948-09-03) (75 лет) Место рождения Ростов-на-Дону, Ростовская область, РСФСР, СССР Страна СССР Украина Россия Научная сфера астроном Место работы ИТАКрымская астрофизическая обсерватория Альма-матер Ростовский...

Не плутати з СБА «Новатор» — бронеавтомобілем від цієї ж компанії на шасі Ford F-550. Спеціалізований броньований автомобіль «Варта» СБА «Варта»Тип бронеавтомобіль/MRAPПоходження УкраїнаІсторія використанняНа озброєнні дониніОператори УкраїнаВійни Війна на сході...

В Википедии есть статьи о других людях с такой фамилией, см. Морозов; Морозов, Владимир. Владимир Морозов Морозов на банкете финала Гран-при (2018) Персональные данные Гражданство Россия Дата рождения 1 ноября 1992(1992-11-01) (31 год) Место рождения Потсдам, Германия Рост 187 см Парт

Untuk kegunaan lain, lihat Kepuh (disambiguasi) KepuhDesaNegara IndonesiaProvinsiJawa BaratKabupatenCirebonKecamatanPalimananKode pos45160Kode Kemendagri32.09.17.2003 Luas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Kepuh adalah desa di kecamatan Palimanan, Cirebon, Jawa Barat, Indonesia. Referensi (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhiran Kode, Data Wilayah Administrasi Pemerintahan, dan Pulau tahun 2021 (Indonesia) P...

Spencer Compton, segundo marqués de Northampton Información personalNombre en inglés Spencer Compton, 2nd Marquess of Northampton Nacimiento 2 de enero de 1790 Fallecimiento 17 de enero de 1851 (61 años)Sepultura Church of St Mary Magdalen, Castle Ashby Nacionalidad BritánicaFamiliaPadres Charles Compton Maria Smith Cónyuge Margaret Douglas-Maclean-Clephane (desde 1815, hasta valor desconocido) EducaciónEducado en Trinity College Información profesionalOcupación Político Cargos...

Опис файлу Опис Фото Джерело В.С.Білецький Час створення 2022 Автор зображення В.С.Білецький Ліцензія див. нижче Я, власник авторських прав на цей твір, добровільно передаю його у суспільне надбання. У випадку, якщо це юридично неможливо, надаю право використовувати це зобр�...

As informações técnicas aqui contidas têm caráter meramente informativo e não devem ser utilizadas como parâmetros para voo real em hipótese alguma. Consulte sempre os manuais originais e atualizados da aeronave. Global Express5000 / 6000 Bombardier Global 5000Um Global Express aterrissando no Aeroporto de Frankfurt Descrição Tipo / Missão Aeronave turbojato monoplano bimotor comercial executiva de uso civil e militar País de origem Canadá Fabricante Bombardier Aerospace Qu...
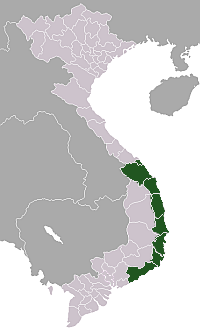
15°41′50″N 108°25′27″E / 15.697086111111°N 108.42407222222°E / 15.697086111111; 108.42407222222 Coordinates: 15°41′49.51″N 108°25′26.66″E / 15.6970861°N 108.4240722°E / 15.6970861; 108.4240722 الساحل الوسط جنوبي ( بالفيتنامية: Nam Trung Bộ ) هي منطقة من مناطق فيتنام. وتتكون من بلدية مستقلة وهي دا نانغ و7 محافظات. محافظات الجنوب نينه توا...

Taman Negara Ansicht des Sungei Tembeling vom Taman NegaraAnsicht des Sungei Tembeling vom Taman Negara Taman Negara (Malaysia) 4.7102.46666666667Koordinaten: 4° 42′ 0″ N, 102° 28′ 0″ O Lage: Malaysia Fläche: 4343 km² Gründung: 1938 Malaysia i3i6 Taman Negara ist ein Nationalpark in Malaysia. Der Name Taman Negara ist malaiisch und heißt übersetzt „National-Park“. Mit seinem 130 Millionen Jahre alten tropischen Dschungel beheimatet der Taman Ne...

2008 anthology by Big Finish The topic of this article may not meet Wikipedia's notability guideline for books. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: The Vampire Curse – news · newspapers · books · sc...
Bagian dari seriKristologi Kristus (Mesias) Putra Allah Allah Putra Kirios Logos Inkarnasi Prawujud Kristus Pribadi Kristus Kemanunggalan Hipostatis Cinta Kasih Kristus Meneladan Kristus Pengetahuan Kristus Syafaat Kristus Kesempurnaan Kristus Tiga Jabatan Kristus Kristologi Lutheran lbs Istilah Yunani Koine Ego eimi (Yunani Ἐγώ εἰμί, pengucapan [eɣó imí]), artinya Akulah atau Itulah aku, adalah sebuah bentuk pengucapan yang dipakai dalam Injil-injil pada bagian firman Yesus ...

Ulvophyceae Klasifikasi ilmiah Kerajaan: Viridiplantae Divisi: Chlorophyta Kelas: UlvophyceaeStewart & Mattox, 1978[1][2] Ordo[3] Bryopsidales Cladophorales Dasycladales Oltmannsiellopsidales Scotinosphaerales Trentepohliales Ulotrichales Ulvales Ulvophyceae atau Ulvophyta adalah kelas dari ganggang hijau. Ulva termasuk dalam kelas ini. Anggota yang cukup dikenal lainnya termasuk Ulothrix, Acetabularia, dan Caulerpa. Anggota lainnya adalah Cladophora, Rhizoclonium ...

Men's singles Squash2014 Commonwealth Games5th Men's singles squash at the Commonwealth GamesLocation Glasgow, ScotlandVenueScotstoun Sports CampusDate(s)24–28 July 2014Websitecwgsquash.netCategoryXX Commonwealth Games ← 2010 2018 → Squash at the2014 Commonwealth GamesSinglesmenwomenDoublesmenwomenmixedvte The Squash at the 2014 Commonwealth Games held at the Scotstoun Sports Campus, Glasgow. Singles play took place from 24 July to 28 July.[1] Nick Matthew...

American college basketball season 2005–06 Texas Longhorns men's basketballBig 12 Season Co-ChampionsNCAA Tournament, Elite EightConferenceBig 12RankingCoachesNo. 9APNo. 9Record30-7 (13-3 Big 12)Head coachRick BarnesHome arenaFrank Erwin CenterSeasons← 2004–052006–07 → 2005–06 Big 12 men's basketball standings vte Conf Overall Team W L PCT W L PCT No. 9 Texas 13 – 3 .813 30 – 7 .811 No. 12 ...

Japanese actress and fashion model Yuko Araki新木 優子Araki in 2016Born (1993-12-15) 15 December 1993 (age 29)Tokyo, JapanOccupations Actress model Years active2007–presentAgentStardust PromotionHeight165 cm (5 ft 5 in) Yuko Araki (新木 優子, Araki Yūko, born 15 December 1993 in Tokyo)[1] is a Japanese actress and fashion model represented by Stardust Promotion. Biography Araki was recruited when she was in elementary school.[2] Her first le...

Zone autonome de Capitol Hill(8 juin – 1er juillet 2020) Capitol Hill Autonomous Zone, CHAZ, CHOP ou Free Cap Hill (en) Le parapluie rose, symbole de la Zone. Administration Pays États-Unis Zone revendiquée Six îlots urbains à proximité du Capitol Hill de Seattle (Washington) Statut politique Micronation sous forme de zone autonome autoproclamée Gouvernement Anarchisme et prises de décisions par consensus journalier Démographie Population 200 hab. (environ) Densité 5 ...

Indian-American activist (1934–2023) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Arun Manilal Gandhi – news · newspapers · books · scholar · JSTOR (May 2023) (Learn how and when to remove this template message) Arun Gandhi2012BornArun Manilal Gandhi(1934-04-14)14 April 1934Durban, Natal Province, South...

Acuerdo de normalización de las relaciones entre Emiratos Árabes Unidos e Israel Anuncio del acuerdo de paz por parte de Donald Trump en el Salón Oval de la Casa Blanca.LocalizaciónPaís Israel Emiratos Árabes UnidosDatos generalesTipo tratado de pazHistóricoFecha 15 de septiembre de 2020[editar datos en Wikidata] El acuerdo de paz entre los Emiratos Árabes Unidos e Israel (o los Acuerdos de Abraham)[1] fue acordado por los Emiratos Árabes Unidos (EAU) e I...

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Outubro de 2012) Centro de Neurociências e Biologia Celular CNC Localização Coimbra Página oficial http://www.cnbc.pt/ O Centro de Neurociências e Biologia Celular (sigla: CNC) é um instituto de investigação de biociências e biome...

1st-century BC Greek historian Diodorus redirects here. For other uses, see Diodorus (disambiguation). Diodorus SiculusDiodorus Siculus as depicted in a 19th-century frescoNative nameΔιόδωροςBornfl. 1st century BCAgira, SicilyLanguageAncient GreekGenreHistoryNotable worksBibliotheca historica Diodorus Siculus or Diodorus of Sicily (Greek: Διόδωρος, translit. Diódōros; fl. 1st century BC) was an ancient Greek historian. He is known for writing the monumental un...
































