Tenseur de Weyl
|
Read other articles:

Peta Chili Santiago, ibu kota Chili Valparaíso La Serena Antofagasta Temuco Talca Arica Chillán Iquique Artikel ini berisi daftar kota di Chili. Sebuah kota didefinisikan oleh Institute Statistik Nasional (INE) Chili sebagai suatu entitas perkotaan (urban)[1] yang memiliki lebih dari 5.000 jiwa penduduk. Daftar ini dibuat menurut laporan Juni 2005 oleh INE, yang berdasarkan sensus 2002 yang mencatat terdapat sebanyak 239 kota di seluruh negeri ini.[2] Daftar kota per region ...

Communist party in Moldova Party of Communists of the Republic of Moldova Partidul Comuniștilor din Republica MoldovaAbbreviationPCRMFirst SecretaryVladimir VoroninExecutive SecretaryOleg ReidmanFounderVladimir VoroninFounded22 October 1993; 30 years ago (1993-10-22)Preceded byCommunist Party of MoldaviaHeadquartersStr. Iorga Nicolae 11, ChişinăuNewspaperComunistulYouth wingKomsomolMembership (2018)11,700[1][needs update]IdeologyCommunismMarxism–Len...

Passport of the United Arab Emirates issued to Emirati citizens Emirati passportThe front cover of a contemporary Emirati biometric passportThe identity information page of a contemporary Emirati biometric passportTypePassportIssued by United Arab Emirates Ministry of Interior: (Regular and Temporary) Ministry of Foreign Affairs: (Diplomatic, Special, and Service)First issued1971 (first version)December 11, 2011 (biometric)PurposeIdentificationEligibilityEmirati citizenshipExpiratio...

محتوى هذه المقالة بحاجة للتحديث. فضلًا، ساعد بتحديثه ليعكس الأحداث الأخيرة وليشمل المعلومات الموثوقة المتاحة حديثاً. (مارس 2019) لمعانٍ أخرى، طالع هجوم دير الزور (توضيح). هجوم دير الزور ( 2017 – 2019)جزء من جزء من الحرب الأهلية السورية، النزاع الكردي السوري–الإسلامي (2013–ا�...
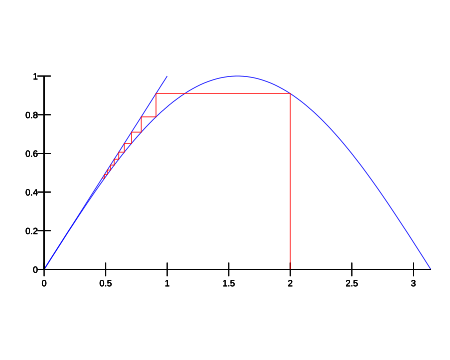
Root-finding algorithm This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fixed-point iteration – news · newspapers · books · scholar · JSTOR (May 2010) (Learn how and when to remove this template message) In numerical analysis, fixed-point iteration is a method of computing fixed points of a function. More spe...

Сен-Мартен-де-ВольсеррSaint-Martin-de-Vaulserre Країна Франція Регіон Овернь-Рона-Альпи Департамент Ізер Округ Ла-Тур-дю-Пен Кантон Кантон-дю-Пон-де-Бовуазен-(Ізер) Код INSEE 38420 Поштові індекси 38480 Координати 45°29′41″ пн. ш. 5°41′00″ сх. д.H G O Висота 320 - 584 м.н.р.м. Площа 3,92

The 1999 Melilla Assembly election was held on Sunday, 13 June 1999, to elect the 2nd Assembly of the Autonomous City of Melilla. All 25 seats in the Assembly were up for election. The election was held simultaneously with regional elections in thirteen autonomous communities and local elections all throughout Spain, as well as the 1999 European Parliament election. Electoral system The Assembly of Melilla was the top-tier administrative and governing body of the autonomous city of Melilla. V...

Jean-Pierre DenisLahir29 Maret 1946 (umur 77)Saint-Léon-sur-l'Isle, PrancisPekerjaanSutradaraPenulis naskahTahun aktif1980-kini Jean-Pierre Denis (lahir 29 Maret 1946) adalah seorang sutradara dan penulis naskah asal Prancis. Ia menyutradarai tujuh film sejak 1980. Debut penyutradaraannya Adrien's Story memenangkan Caméra d'Or di Festival Film Cannes 1980. Film buatannya Field of Honor masuk dalam Festival Film Cannes 1987.[1] Filmografi Adrien's Story (1980) La palombièr...

?Eremodothis Біологічна класифікація Домен: Еукаріоти (Eukaryota) Царство: Гриби (Fungi) Відділ: Аскомікотові гриби (Ascomycota) Клас: Dothideomycetes Родина: Testudinaceae Рід: EremodothisArx Посилання MB: 1879 IF: 1879 Eremodothis — рід грибів родини Testudinaceae. Назва вперше опублікована 1976 року.[1] Класифікація До роду ...

لمعانٍ أخرى، طالع هوراس (توضيح). هوراس الإحداثيات 46°45′35″N 96°54′15″W / 46.759722222222°N 96.904166666667°W / 46.759722222222; -96.904166666667 تاريخ التأسيس 1882 تقسيم إداري البلد الولايات المتحدة[1] التقسيم الأعلى مقاطعة كاس خصائص جغرافية المساحة 28.909509 كيل�...

スピン・ドクターズSpin Doctors 基本情報出身地 アメリカ合衆国 ニューヨーク州ニューヨークジャンル オルタナティヴ・ロック、ファンク・ロック、パワー・ポップ、ジャム・ロック、ブルースロック活動期間 1988年 - 1999年、2001年 - 現在公式サイト www.spindoctors.comメンバー エリック・シャンクマンクリス・バロンアーロン・コメスマーク・ホワイト旧メンバー アンソニ�...

Sporting event delegationIvory Coast at the1992 Summer OlympicsFlag of Ivory CoastIOC codeCIVNOCComité National Olympique de Côte d'Ivoirein BarcelonaCompetitors13 (8 men and 5 women) in 3 sportsMedals Gold 0 Silver 0 Bronze 0 Total 0 Summer Olympics appearances (overview)1964196819721976198019841988199219962000200420082012201620202024 Ivory Coast competed at the 1992 Summer Olympics in Barcelona, Spain. Competitors The following is the list of number of competitors in the Games.[1]...

謝爾蓋·弗拉基米羅維奇·亞斯特列任布斯基 謝爾蓋·弗拉基米羅維奇·亞斯特列任布斯基(俄語:Сергей Владимирович Ястржембский,波蘭語:Siergiej Władimirowicz Jastrzębski,拉丁轉寫:Sergey Vladimirovich Yastrzhembsky),1953年12月4日—),生於莫斯科的波蘭家庭,俄羅斯聯邦政治人物、外交家。1976年畢業於莫斯科國立國際關係學院。 參考來源 外部連結 维基共享资源...

Deputy Speaker of Regional Representative CouncilIncumbentNono SamponoMahyudinSultan Bachtiar Najamudinsince 2 Oktober 2019Formation6 October 2004 This is a list of deputy speakers of the Regional Representative Council, the upper house of Indonesia. This list includes preceding bodies, such as the deputy speaker of the Senate of the United States of Indonesia. Preceding bodies Deputy Speaker of the Senate of the United States of Indonesia Term Portrait Name Assumed office Left office Co...

2008 studio album by SiaSome People Have Real ProblemsStudio album by SiaReleased8 January 2008 (2008-01-08)Recorded2007Genre Pop[1] Length59:15Label Hear Music Monkey Puzzle ProducerJimmy HogarthSia chronology Lady Croissant(2007) Some People Have Real Problems(2008) We Are Born(2010) Alternative cover Singles from Some People Have Real Problems Day Too SoonReleased: 6 November 2007[2] The Girl You Lost to CocaineReleased: 27 March 2008[3] Soon ...

Keuskupan SincelejoDioecesis SinceleiensisLokasiNegaraKolombiaProvinsi gerejawiCartagenaStatistikLuas10.523 km2 (4.063 sq mi)Populasi- Total- Katolik(per 2004)839.770671,816 (80.0%)InformasiRitusRitus LatinPendirian25 April 1969 (54 tahun lalu)KatedralCatedral de San Francisco de Asís(Katedral Santo Fransiskus dari Asisi)Kepemimpinan kiniPausFransiskusUskupNel Hedye Beltrán SantamariaPeta Keuskupan Sincelejo (bahasa Latin: Sinceleiensis) adalah sebuah ...

1991 studio album by Nuclear AssaultOut of OrderStudio album by Nuclear AssaultReleasedSeptember 10, 1991 (1991-09-10)RecordedMarch 26–April 20, 1991StudioThe Hit Factory, New York, New York and Presence Studios, East Haven, ConnecticutGenreThrash metalLength46:04LabelI.R.S.ProducerGlenn Evans, Casey McMackinNuclear Assault chronology Handle with Care(1989) Out of Order(1991) Live at the Hammersmith Odeon(1992) Professional ratingsReview scoresSourceRatingAllMusic[...

Der Titel dieses Artikels ist mehrdeutig. Weitere Bedeutungen sind unter Assisi (Begriffsklärung) aufgeführt. Assisi Assisi (Italien) Staat Italien Region Umbrien Provinz Perugia (PG) Koordinaten 43° 4′ N, 12° 37′ O43.07138888888912.613055555556424Koordinaten: 43° 4′ 17″ N, 12° 36′ 47″ O Höhe 424 m s.l.m. Fläche 186 km² Einwohner 27.880 (31. Dez. 2022)[1] Postleitzahl 06081 Vorwahl 075 ISTAT-Num...

1995 single by You Am ICathy's ClownSingle by You Am Ifrom the album Hi Fi Way ReleasedFebruary 1995StudioGreene St. Recording, New York CityGenreAlternative rockLength2:25LabelrooArtSongwriter(s)Rusty Hopkinson, Andy Kent, Tim RogersProducer(s)Lee RanaldoYou Am I singles chronology When You Got Dry/How Much Is Enough (1994) Cathy's Clown (1995) Jewels and Bullets (1995) Cathy's Clown is the first single from the album Hi Fi Way by Australian rock band, You Am I. It was released in 1995 and w...

This article is about the song. For the film, see Glamour Boy (film). For other uses, see Glamour Boys. 1973 single by The Guess WhoGlamour BoyCover of the 1973 American singleSingle by The Guess Whofrom the album #10 B-sideLie DownReleasedMay 1973Recorded1973GenreRockLength5:27LabelNimbus 9 Records 0977 (CAN)RCA Victor 0977 (US)Songwriter(s)Burton CummingsProducer(s)Jack RichardsonThe Guess Who singles chronology Orly (1973) Glamour Boy (1973) Star Baby (1974) Glamour Boy is a song written b...









