Przestrzeń zupełna
|
Read other articles:

Селище Любешів В'їзна арка садиби (18 ст.) – вигляд із вулиці БондаренкаВ'їзна арка садиби (18 ст.) – вигляд із вулиці Бондаренка Країна Україна Область Волинська область Район Камінь-Каширський район Громада Любешівська селищна громада Код КАТОТТГ: Основні дані Заснован

Airline of the United States Everts Air IATA ICAO Callsign 5V VTS EVERTS Founded1978; 45 years ago (1978)AOC #FXGA030A[1]HubsFairbanks International AirportSecondary hubsTed Stevens Anchorage International AirportFrequent-flyer programN/AFleet size38 (active)12 (in storage)Destinationssee detailsParent companyTatonduk Outfitters LimitedHeadquartersFairbanks, Alaska, United StatesKey peopleRobert W. EvertsWebsitewww.evertsair.com Everts Air is an American airline...

Disambiguazione – Se stai cercando la sillabazione alpha bravo charlie, vedi Alfabeto fonetico NATO. Questa voce o sezione sugli argomenti fonetica e alfabeti non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. L'acronimo in lingua inglese dell'alfabeto fonetico internazionale (IPA) scritto usando l'alfabeto stesso. L'alfabeto fonetico internazionale, i...

МомерстроффMomerstroff Країна Франція Регіон Гранд-Ест Департамент Мозель Округ Форбак-Буле-Мозель Кантон Буле-Мозель Код INSEE 57471 Поштові індекси 57220 Координати 49°09′51″ пн. ш. 6°32′05″ сх. д.H G O Висота 275 - 372 м.н.р.м. Площа 6,17 км² Населення 297 (01-2020[1]) Густ�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (ديسمبر 2019) شحنة محكمة الإغلاقCarga Selladaملصق الفيلممعلومات عامةالصنف الفني دراماتاريخ الصدور28 أغسطس 2015 (2015-08-28) (فنزويلا)25 فبراير 2016 (2016-02-25) (بوليفيا)مد
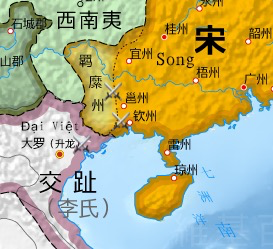
Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin. Mời bạn giúp hoàn thiện bài viết này bằng cách bổ sung chú thích tới các nguồn đáng tin cậy. Các nội dung không có nguồn có thể bị nghi ngờ và xóa bỏ. (tháng 11 năm 2020) Chiến tranh Tống-Việt lần 2nhà Tống (màu cam), Đại Việt (màu tím)Thời gian1075–1077[1]Địa điểmMột phần miền nam Đại Tống[a] và Đại...

Ardito Desio pada tahun 1955 Ardito Desio (18 April 1897 – 12 Desember 2001) ialah seorang geolog, ahli geografi, dan pendaki gunung berkebangsaan Italia. Bertempur dalam Divisi Pendakian selama Perang Dunia I pada tahun 1917 di Bohemia. Kembali ke Italia pada tahun 1918 ia lulus dari Jurusan Geologi Fakultas MIPA di Universitas Firenze pada tahun 1920. Pada tahun 1929 ia ikut serta dalam ekspedisi yang dipimpin oleh Aimone di Savoia (kelak bergelar Tomislav II, Raja Kroasia) ...

Shalin BhanotLahir15 November 1983 (umur 40)[1]Jabalpur, Madhya Pradesh, IndiaPekerjaanAktorTahun aktif2004–sekarangSuami/istriDalljiet Kaur (m. 2009; c. 2015)Anak1 Shalin Bhanot (lahir 15 November 1983) adalah aktor televisi India. Dia berpartisipasi dalam acara realitas tari Nach Baliye 4 dan muncul sebagai pemenang bersama mantan istrinya Dalljiet Kaur. Dia kemudian berpartisipasi dalam acara realitas Bigg Boss 16 di m...

Dutch-American mathematician Prof. Arnold Dresden at Swarthmore College Arnold Dresden (1882–1954) was a Dutch-American mathematician, known for his work in the calculus of variations and collegiate mathematics education.[1][2] He was a president of the Mathematical Association of America and a member of the American Philosophical Society.[3][4] Background Dresden was born in Amsterdam on November 23, 1882, into a wealthy banking family. After matriculating f...

Jeanne IIIPotret oleh François Clouet, 1570Ratu NavarraBerkuasa25 Mei 1555 – 9 Juni 1572Penobatan18 Agustus 1555 di PauPendahuluEnric IIPenerusEnric IIIInformasi pribadiKelahiran16 November 1528[1]Saint-Germain-en-Laye, Kerajaan PrancisKematian9 Juni 1572(1572-06-09) (umur 43)Paris, Kerajaan PrancisPemakamanGereja kadipaten collégiale Saint-Georges, VendômeWangsaAlbretAyahEnric II dari NavarraIbuMarguerite dari NavarraPasangan Wilhelm dari Jülich-Kleve-Berg R...
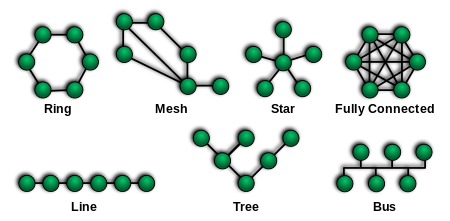
Arrangement of the elements of a communication network This article is about the topology of communication networks. For the topology of electrical networks, see Topology (electrical circuits). For the topology of transport networks, see Transport topology. Part of a series onNetwork science Theory Graph Complex network Contagion Small-world Scale-free Community structure Percolation Evolution Controllability Graph drawing Social capital Link analysis Optimization Reciprocity Closure Homophil...

Czech film director (born 1965) Jan Svěrák Jan Svěrák (Czech pronunciation: [ˈjan ˈsvjɛraːk]) (born 6 February 1965 in Žatec) is a Czech film director. He is the son of screenwriter and actor Zdeněk Svěrák.[1] He studied documentary filmmaking at the FAMU. He and his films have received awards including the Academy Award, Crystal Globe, Golden Globe Award, and Tokyo Grand Prix. He lives in Prague. Filmography Year Czech Title English Title Director Writer Notes 198...

Railway station in Tokyo, Japan KS09 Aoto Station青砥駅Aoto Station entrance in January 2008General informationLocation3-36-1 Aoto, Katsushika-ku, TokyoJapanOperated by Keisei Electric RailwayLine(s) KS Keisei Main Line KS Keisei Oshiage Line Platforms2 island platformsTracks4ConnectionsBus stopOther informationStation codeKS09HistoryOpened1 November 1928PassengersFY201547,719 daily[1] Services Preceding station Keisei Following station NipporiKS02towards Keisei Ueno Skyliner(limit...

Record label, founded 1988, absorbed into Warner Classics from 2013 Virgin ClassicsParent companyThorn EMI (1992–1996)EMI (1996–2012)Parlophone Label Group(independent operation; 2012–2013)Warner Music Group(back catalogue; 2013–present)Founded1988; 35 years ago (1988)FounderRichard BransonDefunct2013; 10 years ago (2013)StatusDefunct; absorbed into Erato RecordsGenreClassical musicCountry of originFrance Virgin Classics was a record label founded i...

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada.Puedes avisar al redactor principal pegando lo siguiente en su página de discusión: {{sust:Aviso referencias|Lenguas de Francia}} ~~~~Este aviso fue puesto el 17 de agosto de 2023. Mapa de las lenguas regionales de Francia y Bélgica. Las lenguas de Francia comprenden las lenguas habladas por la población que reside en territorio francés, es decir, el territorio de la Francia metropolitana y los te...

This article's factual accuracy may be compromised due to out-of-date information. Please help update this article to reflect recent events or newly available information. (August 2010) MSI Wind NetbookAn image of a 2008 Computex MSI Wind NotebookDeveloperMicro-Star InternationalTypeSubnotebook/NetbookMedia80, 120, 160 or 250 GB 2.5 HDDOperating systemWindows 7 Starter, Windows XP, LinuxCPUIntel Atom @ 1.60 / 1.66 GHz (N270, N280, N450)Memory1 GB (Linux) or 1 GB / 2 GB (Windows)Display10...

1842 treaty between Qing China and Britain Treaty of NankingTreaty of Peace, Friendship, and Commerce Between Her Majesty the Queen of Great Britain and Ireland and the Emperor of China[1]Signing of the treaty on board HMS CornwallisSigned29 August 1842 (1842-08-29)LocationNanjing (Nanking), Qing EmpireEffective26 June 1843 (1843-06-26)ConditionExchange of ratificationsParties Qing Empire United Kingdom LanguagesEnglish and ChineseFull text Treaty o...

Israeli yeshiva program combining Torah study and military service Beit Midrash of the Kerem B'Yavneh hesder yeshiva Hesder (Hebrew: הסדר arrangement; also Yeshivat Hesder ישיבת הסדר) is an Israeli yeshiva program which combines advanced Talmudic studies with military service in the Israel Defense Forces, usually within a Religious Zionist framework. The program allows Orthodox Jewish men to serve in the Israeli military while still engaging in Torah study. Description Hes...

2006 single by GodsmackThe EnemySingle by Godsmackfrom the album IV ReleasedOctober 31, 2006Recorded2005Genre Heavy metal alternative metal Length4:07LabelRepublic/UniversalSongwriter(s)Sully ErnaProducer(s)Sully Erna, Andy JohnsGodsmack singles chronology Shine Down (2006) The Enemy (2006) Good Times Bad Times (2007) The Enemy is a song by American rock band Godsmack and the last single from their album IV. After its release in October 2006, the song landed at number four on the Mainstream R...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (February 2009) (Learn how and when to remove this template message) 33d Troop Carrier Squadron(currently Air Mobility Command Test and Evaluation Squadron)Active1942–1946; 1994-presentCountry United StatesBranch United States Air ForceRoleTest and evaluationPart ofAir Mobility CommandGarrison/HQ...



![{\displaystyle (0,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/847a4aff00dc9dc9db8eb8b54889eab06a8787e3)






















