Share to: share facebook share twitter share wa share telegram print page

VSEPR

VSEPR (ang. Valence Shell Electron Pair Repulsion – odpychanie par elektronowych powłoki walencyjnej). Metoda ta została zaprezentowana w 1940 roku przez Nevila Sidgwicka(inne języki) i Herberta Powella(inne języki)[1]. Według niej o budowie przestrzennej cząsteczki decyduje łączna liczba elektronów walencyjnych wokół atomu centralnego oraz orientacja przestrzenna obszarów orbitalnych, w których mieszczą się te elektrony.

Teoria VSEPR zakłada, że pary elektronów są rozmieszczone wokół atomu centralnego tak, aby siły wzajemnego odpychania były możliwie jak najmniejsze, przy czym w sumarycznym efekcie wszystkich odpychań istotny jest udział wolnych (niewiążących) i wiążących par elektronowych. Najsłabiej odpychają się pary wiążące, potem para wiążąca z wolną parą elektronową, a najsilniej dwie wolne pary elektronowe. Inaczej mówiąc, jeżeli odległości par decydujących o geometrii cząsteczki są maksymalne, to w zależności od liczby tych par powstają pewne uprzywilejowane struktury o charakterystycznym rozmieszczeniu wolnych i wiążących par elektronowych na wyróżnionych kierunkach wokół atomu centralnego.

Regularne kształty cząsteczek powstają tylko wtedy, gdy wszystkie pary elektronów wiążących zostaną wykorzystane do związania takich samych atomów. Występowanie w cząsteczce różnych ligandów wokół atomu centralnego i niewiążących par elektronowych zaburza idealne struktury, np. wraz z rosnącą liczbą wolnych par elektronowych może następować zmiana kąta wiązania.

W niektórych przypadkach metoda VSEPR nie nadaje się do przewidywania budowy przestrzennej związków, gdyż nie prowadzi do prawidłowego opisu ich struktury, np. nie jest wygodne zastosowanie jej do opisu budowy cząsteczek zawierających wiązania zdelokalizowane.

Opis koncepcji

Właściwości i geometrię cząsteczek typu ABn można opisać, przyjmując że:

  • A jest atomem centralnym i n atomów B (jednakowych bądź różnych), zwanych roboczo ligandami, uczestniczy w tworzeniu orbitali molekularnych z atomem A
  • cząsteczka zawiera pierwiastki grup głównych układu okresowego
  • hybrydyzacji ulegają orbitale atomu centralnego A
  • jeżeli cząsteczka zawiera więcej niż jeden atom centralny to hybrydyzacji ulegają wszystkie atomy centralne (jak np. C w etenie CH
    2    =CH
    2    )

Wśród elektronów walencyjnych atomu centralnego wyróżnia się:

  • wolne pary elektronowe danego atomu (zlokalizowane w polu jednego jądra) - stanowią pary niewiążące
  • elektrony, które są wspólne dla dwóch sąsiadujących atomów - stanowią pary wiążące (pary zlokalizowane w polu dwóch sąsiadujących jąder)

Wśród par wiążących wyróżnić można pary σ i pary π, które mogą tworzyć:

  • wiązania typu σ (o symetrii względem osi łączącej jądra)
  • wiązania typu π (o obszarze orbitalnym złożonym z dwóch fragmentów leżących poza osią łączącą jądra)

Określonym wartościom liczby przestrzennej oznaczanej symbolem Lp, równej liczbie orbitali zhybrydyzowanych (LH), odpowiada określona geometria cząsteczka. O kształcie cząsteczki decyduje liczba wiążących par elektronowych (PW) i wolnych par elektronowych (WPE). Ich suma wskazuje typ hybrydyzacji, a tym samym podstawowy wielościan koordynacyjny, którego naroża zajmują atomy lub wolne pary elektronowe:

Lp = σPW + WPE = LH

gdzie:

  • σPW - liczba par elektronowych tworzących wiązanie σ; wynosi ona tyle, ile atomów B jest przyłączonych do atomu centralnego A.
    Przykład: dla PCl
    5     σPW = 5, dla H
    2    O     σPW = 2, dla COCl
    2     σPW = 3,
  • WPE - liczba wolnych par elektronowych atomu centralnego; oblicza się ją odejmując od liczby elektronów walencyjnych atomu centralnego A, taką liczbę elektronów, jaka jest potrzebna do uzupełnienia konfiguracji wszystkich atomów B i dzieli przez 2, czyli WPE = 1/2 [liczby elektronów walencyjnych atomu A pomniejszona o liczbę elektronów potrzebną do uzupełnienia oktetów (lub dubletów dla wodoru) dla n atomów B]. Dla jonów ujemnych zwiększa się, a dla jonów dodatnich zmniejsza się liczbę elektronów walencyjnych o ładunek jonu.
    Przykład: Dla H
    2    O     WPE = (6-2)/2 = 2, dla SO2−
    4     WPE = (6+2−8)/2 = 0.

Wartość liczby przestrzennej możemy ustalić:

  • ze wzoru elektronowego cząsteczki
  • przez zsumowanie liczby wolnych par elektronowych atomu centralnego z liczbą par elektronowych tworzących wiązania σ (równej liczbie atomów B przyłączonych do atomu centralnego)

Ostatni etap opisu budowy przestrzennej cząsteczki opiera się na fakcie, że do każdej wartości Lp jest przyporządkowana charakterystyczna struktura przestrzenna. Można więc powiedzieć, że przestrzenna budowa cząsteczki, a zatem kierunki, w jakich ustawiają się ligandy i wolne pary elektronowe, są określone liczbą przestrzenną.

Zależność między liczbą wolnych i wiążących par elektronowych a kształtem cząsteczki według modelu VSEPR zebrano w tabeli:

Typ Cząsteczki:

A - atom centralny
X - ligandy
E - wolne pary elektronowe

Liczba przestrzenna Typ hybrydyzacji Kształt cząsteczki Rozmieszczenie elektronów

(na żółto zaznaczono wolne pary elektronowe)

Geometria cząsteczki Przykłady
AX1En cząsteczka dwuatomowa HF, O
2
AX2E0 2 sp linia BeCl
2, HgCl
2, CO
2
AX2E1 3 sp2 Kształt litery V NO−
2, SO
2, O
3
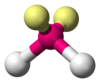
AX2E2 4 sp3 Kształt litery V H
2O, OF
2
AX2E3 5 sp3d[2] linia XeF
2, I−
3
AX3E0 3 sp2 trójkąt równoboczny BF
3, CO2−
3, NO−
3, SO
3
AX3E1 4 sp3 piramida trygonalna NH
3, PCl
3
AX3E2 5 sp3d[2] kształt litery T ClF
3, BrF
3
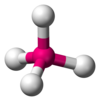
AX4E0 4 sp3 tetraedr CH
4, PO3−
4, SO2−
4, ClO−
4
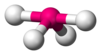
AX4E1 5 sp3d[2] zdeformowany tetraedr SF
4
AX4E2 6 sp3d2[2] kwadrat, płaski XeF
4
AX5E0 5 sp3d[2] bipiramida trygonalna PCl
5
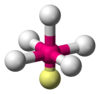
AX5E1 6 sp3d2[2] piramida kwadratowa ClF
5, BrF
5
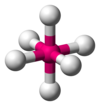
AX6E0 6 sp3d2[2] oktaedr SF
6
AX6E1 7 sp3d3[2] piramida pentagonalna XeF
6
AX7E0 7 sp3d3[2] bipiramida pentagonalna IF
7
Liczba
przestrzenna 		kształt cząsteczki
brak wolnych par elektronowych 		1 wolna para elektronowa 2 wolne pary elektronowe 3 wolne pary elektronowe
2
linia
      
3
trójkąt równoboczny
Kształt litery V
    
4
tetraedr
piramida trygonalna
Kształt litery V
  
5
bipiramida trygonalna
zdeformowany tetraedr
kształt litery T
liniowy
6
oktaedr
piramida kwadratowa
kwadrat, płaski
  
7
bipiramida pentagonalna
piramida pentagonalna
    

Poniżej podano przykłady obliczeń odpowiednich parametrów, dzięki którym, przy zastosowaniu metody VSEPR, można określić budowę cząsteczki:

Atom centralny Wolne pary elektronowe Liczba przestrzenna

Lp= PW + WPE

typ hybrydyzacji kształt
C w CH
4 		(4−4x1)/2 = 0 4+0=4 sp3 Tetraedr
O w H
2O 		(6−2x1)/2=2 2+2=4 sp3 Kształt litery V
N w NH
3 		(5−3x1)/2=1 3+1=4 sp3 Piramida trygonalna
S w SO
2 		(6−2x2)/2=1 2+1=3 sp2 Kształt litery V
C w CO2−
3 		(4−3x2+2)/2=0 3+0=3 sp2 trójkąt równoboczny
C w CO
2 		(4−2x2)/2=0 2+0=2 sp liniowa

Przypisy

  1. ↑ N.V. Sidgwick, H.M. Powell, Bakerian Lecture. Stereochemical Types and Valency Groups, „Proceedings of the Royal Society of London. Series A”, 176, 1940, s. 153–180, JSTOR: 97507 (ang.).
  2. ↑ a b c d e f g h i Według współczesnych poglądów, rzeczywisty udział orbitali d w wiązaniu jest znikomy. Zob. np. John Morrison Galbraith, On the role of d orbital hybridization in the chemistry curriculum, „Journal of Chemical Education”, 84 (5), 2007, s. 783-787, DOI: 10.1021/ed084p783 (ang.).

Linki zewnętrzne
Kembali kehalaman sebelumnya