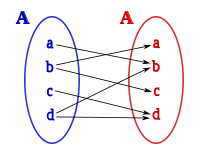
Relação binária
|
Read other articles:

Гаспар ВієссюНародився 18 лютого 1746(1746-02-18)[1][2]Женева, Женева, ШвейцаріяПомер 21 жовтня 1814(1814-10-21)[2] (68 років)Країна Республіка Женева Перша французька республіка Перша Французька імперіяДіяльність неврологРодичі André-Frédéric Puerarid[3] Гаспар Вієссю (фр. Gaspar...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2022) غابرييلا سيرا معلومات شخصية اسم الولادة (بالكتالونية: Gabriela Serra i Frediani) الميلاد 18 ديسمبر 1951 (72 سنة) ماتارو، برشلونة[1] مواطنة إسبانيا منا�...

Este artigo não cita fontes confiáveis. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Novembro de 2012) O Royal Army Service Corps (RASC) foi um quartel do exército britânico responsável por transporte terrestre, costal e lacustre. Este artigo é um esboço. Você pode ajudar a Wikipédia expandindo-o. Editor: considere marcar com um esboço ...

Ortler-Alpen Ortlergruppe Höchster Gipfel Ortler (3905 m s.l.m.) Lage Provinzen Bozen – Südtirol, Brescia, Sondrio, Trient in Italien und Kanton Graubünden in der Schweiz Teil der Zentralalpen/Südalpen Einteilung nach AVE 48a <--Ortlergipfel--> Koordinaten 46° 31′ N, 10° 33′ O46.51055555555610.5419444444443905Koordinaten: 46° 31′ N, 10° 33′ O Gestein Kalkgestein und Quarzphyllit f1 Die Ortler-Alpen, auch Ortlergruppe, i...

Hubbelsche Ansicht vom Damm des Mittellandkanals Ansicht vom Damm des Mittellandkanals Lage Garbsen und Seelze in der niedersächsischen Region Hannover Fläche 14 ha Kennung NSG HA 255 WDPA-ID 555700703 Geographische Lage 52° 24′ N, 9° 35′ O52.40589.5802Koordinaten: 52° 24′ 21″ N, 9° 34′ 49″ O Hubbelsche (Niedersachsen) Einrichtungsdatum 6. Dezember 2019 f6 Die Hubbelsche ist ein zwischen den Städten Seelze und Garb...

Marvel Comics supervillain Comics character Matt MurdockThe KingpinTextless cover of Spider-Gwen vol. 2 #28 (January 2018). Art by Robbi Rodriguez.Publication informationPublisherMarvel ComicsFirst appearanceEdge of Spider-Verse #2 (September 2014)Created by Jason Latour Robbi Rodriguez (Based upon Daredevil by Stan Lee and Bill Everett) In-story informationAlter egoMatthew Michael MurdockSpeciesHuman MutatePlace of originQueens, New York City, Earth-65Team affiliations The Hand The Chaste S....

Yarnton Manor, the former location of the Oxford Centre for Hebrew and Jewish Studies The Oxford Centre for Hebrew and Jewish Studies (OCHJS) is a recognised independent centre of the University of Oxford, England. Its research fellows teach on a variety of undergraduate and master's degrees in Oriental studies, and it publishes the Journal of Jewish Studies. History and case statement The centre was founded in 1972 by Dr David Patterson to help restore Jewish Studies in Europe in the afterma...

Титульний лист першого тому Національного біографічного словника (1885) Національний біографічний словник (англ. Dictionary of National Biography, DNB) — стандартний довідковий посібник щодо відомих діячів британської історії, що публікується від 1885 року. Оновлений Оксфордський націон

Zodiac KillerSketsa Zodiac KillerPembunuhanJumlah korban5 dipastikan tewas, 2 terluka, mungkin 20–28 total pembunuhan (diklaim telah membunuh 37 orang)Waktu pembunuhan1960–1970NegaraAmerika SerikatNegara bagianCalifornia, kemungkinan juga Nevada Zodiac Killer adalah julukan untuk pembunuh berantai dari Amerika Serikat[1] yang beroperasi di California Utara pada akhir tahun 1960-an dan awal tahun 1970-an. Identitasnya belum diketahui sampai hari ini. Kata Zodiac digunakan oleh sang...

Este artículo o sección tiene referencias, pero necesita más para complementar su verificabilidad.Este aviso fue puesto el 8 de junio de 2007. Catedral Metropolitana de Santiago durante el Te Deum de 2010. El Te Deum Ecuménico de Fiestas Patrias es una liturgia de acción de gracias realizada en Chile cada 18 de septiembre (a las 11 horas) en la Catedral Metropolitana de Santiago desde 1811, con ocasión de las Fiestas Patrias que se celebran en ese país. En él participan las máximas a...

Polish media company This article's factual accuracy may be compromised due to out-of-date information. Please help update this article to reflect recent events or newly available information. (February 2020) AgoraAgora's headquarters in Warsaw.TypePublicTraded asWSE: AGOLSE: 0MNMIndustryMass mediaFoundedWarsaw, Poland (1989)HeadquartersWarsaw, PolandKey peopleBartosz Hojka (Executive Chairman)Adam Michnik (Co-founder)ProductsGazeta WyborczaRevenue PLN 836.5 million (2020)[1]...

1773 American protest against British taxation For other uses, see Boston Tea Party (disambiguation). Boston Tea PartyPart of the American RevolutionSource: W. D. Cooper. Boston Tea Party in The History of North America. London: E. Newberry, 1789. Engraving. Plate opposite p. 58. Rare Book and Special Collections Division, Library of Congress (40)DateDecember 16, 1773; 249 years ago (1773-12-16)LocationBoston, Province of Massachusetts Bay, British AmericaCaused byTea ActGoa...

Cohort born from 1883 to 1900 For other uses, see Lost Generation (disambiguation). Part of a series onSocial generations of the Western world Lost Generation Greatest Generation Silent Generation Baby boomers Generation X Millennials Generation Z Generation Alpha vte The Lost Generation was the social generational cohort in the Western world that was in early adulthood during World War I. The generation is generally defined as people born from 1883 to 1900, and came of age in either the 1900...

Municipality in South, BrazilBraço do NorteMunicipality FlagSealLocation in Santa CatarinaCoordinates: 28°16′30″S 49°09′57″W / 28.275°S 49.1658°W / -28.275; -49.1658Country BrazilRegionSouthStateSanta CatarinaMesoregionSul CatarinensePopulation (2020 [1]) • Total33,876Time zoneUTC -3Area code+55 48Websitebracodonorte.sc.gov.br Braço do Norte is a municipality in the state of Santa Catarina in the South region of Brazil. Most ...

HAL/Turbomeca Shakti (disebut Ardiden 1H oleh Turbomeca) adalah mesin helikopter turboshaft Amerika dari tahun 2000-an yang dikembangkan bersama oleh India dan Prancis. Aplikasi HAL Dhruv HAL Light Combat Helicopter Kamov Ka-62 - Ardiden 3G[1] Referensi ^ Butowski, Piotr. Turbomeca Ardiden Diarsipkan 2013-02-05 di Archive.is Turbomeca Ardiden 1H Diarsipkan 2014-05-08 di Wayback Machine. Armytechnology.com: Advanced Light Helicopter Diarsipkan 2016-03-03 di Wayback Machine.

Provinsi Hoa Binh merupakan sebuah provinsi di Vietnam. Provinsi ini terletak di bagian barat laut di negara itu. Provinsi ini memiliki luas wilayah 4.662 km² dengan memiliki jumlah penduduk 803.300 jiwa (2004). Provinsi ini memiliki angka kepadatan penduduk 172 jiwa/km². Ibu kotanya ialah Hoa Binh. Pembagian administrasi Hòa Bình - ibu kota Đà Bắc Mai Châu Kỳ Sơn Cao Phong Lương Sơn Kim Bôi Tân Lạc Lạc Sơn Lạc Thủy Yên Thủy Pranala luar Situs resmi Diarsipka...

This article is about the Wir sind Helden song. For the Hardy Caprio and Digdat song, see Hardy Caprio § As lead artist. 2002 single by Wir sind HeldenGuten TagSingle by Wir sind Heldenfrom the album Die Reklamation ReleasedNovember 18, 2002 (EP)February 3, 2003 (single)Recorded2002StudioFreundenhaus, BerlinGenre Pop rock Length3:36LabelEMISongwriter(s) Judith Holofernes Jean-Michel Tourette Pola Roy Producer(s)Patrik MajerWir sind Helden singles chronology Guten Tag (2002) Müssen Nur ...

List of cyclists The 2015 national road cycling championships began in Australia with the time trial event (both men and women) on 8 January, as is tradition. Jerseys The winner of each national championship wears the national jersey in all their races for the next year in the respective discipline, apart from the World Championships and the Olympics, or unless they are wearing a category leader's jersey in a stage race. Most national champion jerseys tend to represent a country's flag or use...

Exposición de la Revolución Fascista UbicaciónPaís ItaliaLocalidad RomaCoordenadas 41°53′58″N 12°29′24″E / 41.899444444444, 12.49[editar datos en Wikidata] La Exposición de la Revolución Fascista (italiano: Mostra della Rivoluzione Fascista) fue un espectáculo celebrado en Roma en el Palazzo delle Esposizioni de 1932 a 1934.[1] Inaugurada por Benito Mussolini el 28 de octubre de 1932, tuvo 4 millones de visitantes. Se repitió en las dos...

Type of crystal structure This article is about the synthetic compounds. For the mineral, see Perovskite. Structure of a perovskite with general chemical formula ABX3. The red spheres are X atoms (usually oxygens), the blue spheres are B atoms (a smaller metal cation, such as Ti4+), and the green spheres are the A atoms (a larger metal cation, such as Ca2+). Pictured is the undistorted cubic structure; the symmetry is lowered to orthorhombic, tetragonal or trigonal in many perovskites.[1&...