Forța Coriolis
|
Read other articles:
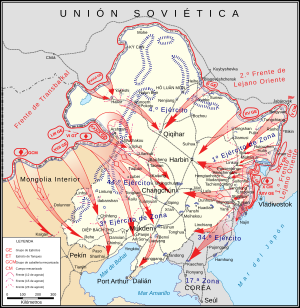
Манчжурська операція Радянсько-японська війна Дата: 9 серпня — 2 вересня 1945 Місце: Маньчжурія Результат: перемога СРСР Сторони СРСР МНР Японська імперія Маньчжурська держава Менцзян Командувачі Василевський Олександр Михайлович, Малиновський Родіон Якович, Мерецков...

Church in Massachusetts, United StatesOur Lady of Czestochowa Parish42°15′6″N 71°47′53″W / 42.25167°N 71.79806°W / 42.25167; -71.79806Location34 Ward StreetWorcester, MassachusettsCountryUnited StatesDenominationRoman CatholicWebsiteParish websiteHistoryFounded29 November 1906 (1906-11-29)Founder(s)Polish immigrantsDedicationOur Lady of CzestochowaAdministrationDivisionCluster 42ProvinceBostonDioceseWorcesterClergyBishop(s)Most Rev. Robert Jo...

العلاقات الأذربيجانية السنغافورية أذربيجان سنغافورة أذربيجان سنغافورة تعديل مصدري - تعديل العلاقات الأذربيجانية السنغافورية هي العلاقات الثنائية التي تجمع بين أذربيجان وسنغافورة.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية

Países Bajos14.º puesto Titular Alternativa Datos generales Asociación KNVB Confederación UEFA Seudónimo Los tulipanes Participación 2.ª Mejor resultado Octavos de final (1934) Entrenador Bob Glendenning Estadísticas Partidos 1 Goles anotados 0 Goles recibidos 3 Goleador - Cronología Anterior Italia 1934 Siguiente Alemania Federal 1974 Países Bajos fue una de las 15 selecciones participantes de la Copa Mundial de Fútbol de Francia 1938, la cual fue su segunda participación consecu...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Comparative air force enlisted ranks of Africa – news · newspapers · books · scholar · JSTOR (October 2021) (Learn how and when to remove this template message) Rank comparison of non-commissioned officers and enlisted personnel for air forces of African states...

Magazine This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Runner's World – news · newspapers · books · scholar · JSTOR (October 2011) (Learn how and when to remove this template message) Runner's WorldSerena Burla on cover of the July 2011 issueRunner-in-ChiefJeff DengateFormer editorsDavid WilleyCategoriesHe...

Pamphlet written by Daniel Dulany the Younger Considerations on the Propriety of Imposing Taxes in the British Colonies, for the Purpose of Raising a Revenue, by Act of Parliament Title page of a London reprint of the pamphletAuthorDaniel Dulany the YoungerCountryBritish EmpireLanguageEnglishPublished1765 Considerations on the Propriety of Imposing Taxes in the British Colonies was a pamphlet written by Daniel Dulany the Younger in opposition to the Stamp Act of 1765.[1] In the pamphl...

Sebuah kontrak yang ditulis dalam bahasa Tionghoa dan Sinkang, tahun 1784. Naskah Sinkang (Hanzi: 新港文書; Pinyin: Xīngǎng wénshū; Wade–Giles: Hsin-kang wen-shu; juga dieja Sinkan atau Sinckan) adalah kumpulan catatan sewa, hipotek, dan perjanjian perdagangan lainnya yang ditulis dalam bahasa Sinkang, Taivoan, dan Makatao. Naskah-naskah ini juga biasanya disebut sebagai kontrak Fanzi (Hanzi: 番仔契; Pinyin: Fānzǐ Qì; Pe̍h-ōe-jī: hoan-á-khè). Beber...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Chargeabilitas atau M (bahasa Inggris: chargeability) merupakan kemampuan suatu batuan atau material untuk menyimpan arus listrik sesaat yang mengenainya. Arus listrik sesaat ini terbentuk akibat adanya efek elektrokimia pada batuan. Dalam ilmu geofisi...

Klip en bloc dimasukan langsung ke senapan M1 Garand Klip adalah alat yang digunakan untuk menyimpan beberapa butir amunisi bersama-sama menjadi satu kesatuan, klip yang telah dipasangi amunisi kemudian dimasukan kedalam magazen atau silinder senjata api. Penggunaan klip berguna untuk mempercepat proses pengisian amunisi ke dalam senjata api, karena dengan menggunakan klip, amunisi akan dapat dimuat sekaligus ke dalam magazen atau silinder senjata api. Dari berbagai jenis klip yang ada, beber...

Tanzania en los Juegos Olímpicos Bandera de TanzaniaCódigo COI TANCON Comité Olímpico de TanzaniaMedallas 0 2 0 2 Historia olímpicaJuegos de verano 1964* • 1968 • 1972 • 1976 • 1980 • 1984 • 1988 • 1992 • 1996 • 2000 • 2004 • 2008 • 2012 • 2016 • 2020 • *Participó como Tanganica[editar datos en Wikidata] El Comité...

Fictional character from the soap opera Coronation Street Soap opera character Cilla Battersby-BrownCoronation Street characterPortrayed byWendi PetersDuration2003–2007, 2014First appearanceEpisode 560720 October 2003Last appearanceEpisode 851314 November 2014ClassificationFormer; regularIntroduced byKieran Roberts (2003)Stuart Blackburn (2014)Spin-offappearancesCoronation Street: Out of Africa (2008)In-universe informationOccupationBarmaidCatering assistantNurseHusbandL...

1972 Indian filmKadhalikka VangaTitle cardDirected byI. N. MurthyStory byTamilvananProduced byTamilvananStarringJaishankar Major Sundarrajan Thengai Srinivasan Manorama Srikanth ShabnamCinematographyChitti BabuEdited byK. BaluMusic byRaghava NaiduProductioncompanyComedy PicturesRelease date 25 February 1972 (1972-02-25) Running time149 minutesCountryIndiaLanguageTamil Kadhalikka Vanga (transl. Come to love) is a 1972 Indian Tamil language film produced and written by Tami...

Church in Florence, Italy For the perfumery and wellness apothecary, see Officina Profumo-Farmaceutica di Santa Maria Novella. For the railway station, see Firenze Santa Maria Novella railway station. Basilica of Santa Maria NovellaBasilica di Santa Maria Novella (Italian)The façade of Santa Maria Novella, completed by Leon Battista Alberti in 1470ReligionAffiliationCatholicDistrictArchdiocese of FlorenceEcclesiastical or organizational statusMinor basilicaYear consecrated1420LocationLo...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (December 2016) Compañía General de Tabacos de Filipinas v. Collector of Internal RevenueCourtUS Supreme CourtDecided21 November 1927Citation(s)275 US 87 (1927)KeywordsPreemption Compañía General de Tabacos de Filipinas v. Collector of Internal Revenue, 275 US 87 (1927) is a US tax law case during the Lochner era of the US Supreme C...

For other films related with Aladdin, see Aladdin (disambiguation) § Films. 2009 Indian filmAladinTheatrical release posterDirected bySujoy GhoshWritten bySujoy GhoshRitesh Shah Suresh Nair (additional story)Screenplay bySujoy GhoshProduced bySujoy GhoshSunil A LullaStarringAmitabh BachchanSanjay DuttRitesh DeshmukhJacqueline FernandezNarrated byBoman IraniCinematographySirsha RayEdited bySuresh PaiMusic byScore:Jody J JenkinsSongs:Vishal–ShekharProductioncompanyBoundscript Motion Pic...

Mythological interpretations of the origin of the Milky Way Great Sky River redirects here. For the novel, see Great Sky River (novel). This article is about mythology related to the Milky Way Galaxy. For other uses, see Milky Way (disambiguation). The Galactic Center as seen from Earth's night sky There are many myths and legends about the origin of the Milky Way, the crowd of stars that makes a distinctive bright streak across the night sky. Mythology among cultures Armenian Ancient Armenia...

Para Putra dan Pujaan Hati PengarangD. H. LawrenceNegaraBritania RayaBahasaInggrisGenreNovel otobiografiPenerbitGerald Duckworth and Company LtdTanggal terbit1913[1]Halaman423Didahului olehThe Trespasser Diikuti olehThe Rainbow TeksPara Putra dan Pujaan Hati di Wikisource Para Putra dan Pujaan Hati adalah sebuah novel karya D. H. Lawrence.[2] Ceritanya menelusuri konflik emosional melalui Paul Morel, dan hubungannya yang menegangkan dengan seorang ibu ...

Адыге Республикэм и ГимнLagu kebangsaan Republik AdygeaPenulis lirikIskhak Shumafovich MashbashKomponisUmar Khatsitsovich TkhabisimovPenggunaan1992Sampel audioLagu kebangsaan Republik Adygeaberkasbantuan Lagu Kebangsaan Adygea dalam bahasa Rusia Rekaman instrumental dari lagu kebangsaan Lagu Republik Adygea, lirik di tulis oleh Iskhak Shumafovich Mashbash, dan komposer musiknya oleh Umar Khatsitsovich Tkhabisimov. Lirik Dalam bahasa Adyghe АДЫГЕ РЕСПУБЛИКЭ�...

Style of French architecture French Renaissance architectureTop: Château de Chambord; Château de Chenonceau: Center: Azay le Rideau; Château de Fontainebleau; Bottom: Lescot Wing of LouvreYears activeLate 15th – early 17th centuries French Renaissance architecture is a style which was prominent between the late 15th and early 17th centuries in the Kingdom of France. It succeeded French Gothic architecture. The style was originally imported from Italy after the Hundred Years' War by the F...






























































