 –Ф–µ–ї—М—В–Њ–Є–і–∞
–Ф–µ–ї—М—В–Њ–Є–і–∞
–Ф–µ–ї—М—В–Њ–Є–і–∞ (–Є–ї–Є –Ї—А–Є–≤–∞—П –®—В–µ–є–љ–µ—А–∞) вАФ –њ–ї–Њ—Б–Ї–∞—П –∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–∞—П –Ї—А–Є–≤–∞—П, –Њ–њ–Є—Б—Л–≤–∞–µ–Љ–∞—П —Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ–Њ–є —В–Њ—З–Ї–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Ї–∞—В—П—Й–µ–є—Б—П –њ–Њ –≤–љ—Г—В—А–µ–љ–љ–µ–є —Б—В–Њ—А–Њ–љ–µ –і—А—Г–≥–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, —А–∞–і–Є—Г—Б –Ї–Њ—В–Њ—А–Њ–є –≤—В—А–Њ–µ –±–Њ–ї—М—И–µ —А–∞–і–Є—Г—Б–∞ –њ–µ—А–≤–Њ–є.
–Ф–µ–ї—М—В–Њ–Є–і–∞ —П–≤–ї—П–µ—В—Б—П —З–∞—Б—В–љ—Л–Љ —Б–ї—Г—З–∞–µ–Љ –≥–Є–њ–Њ—Ж–Є–Ї–ї–Њ–Є–і—Л –њ—А–Є  .
.
–Ш—Б—В–Њ—А–Є—П
–Ю–±—Л—З–љ—Л–µ —Ж–Є–Ї–ї–Њ–Є–і—Л –±—Л–ї–Є –Є–Ј—Г—З–µ–љ—Л –У–∞–ї–Є–ї–µ–Њ –У–∞–ї–Є–ї–µ–µ–Љ –Є –Ь–∞—А–Є–љ–Њ–Љ –Ь–µ—А—Б–µ–љ–љ–Њ–Љ (Marin Mersenne) –µ—Й–µ –≤ 1599 –≥–Њ–і—Г, –љ–Њ —Б–њ–µ—Ж–Є–∞–ї—М–љ—Л–µ —Ж–Є–Ї–ї–Њ–Є–і–∞–ї—М–љ—Л–µ –Ї—А–Є–≤—Л–µ –±—Л–ї–Є –≤–њ–µ—А–≤—Л–µ —А–∞—Б—Б–Љ–Њ—В—А–µ–љ—Л –Ю–ї–µ –†–µ–Љ–µ—А–µ–Љ (Ole R√Єmer) –≤ 1674 –≥–Њ–і—Г –њ—А–Є –Є–Ј—Г—З–µ–љ–Є–Є –ї—Г—З—И–µ–є —Д–Њ—А–Љ—Л –Ј—Г–±—М–µ–≤ –і–ї—П –Ј—Г–±—З–∞—В—Л—Е –Ї–Њ–ї–µ—Б. –Ы–µ–Њ–љ–∞—А–і –≠–є–ї–µ—А –≤–њ–µ—А–≤—Л–µ —Г–њ–Њ–Љ–Є–љ–∞–µ—В –љ–∞—Б—В–Њ—П—Й—Г—О –і–µ–ї—М—В–Њ–Є–і—Г –≤ 1745 –≥–Њ–і—Г –≤ —Б–≤—П–Ј–Є —Б –Ј–∞–і–∞—З–µ–є –Є–Ј –Њ–њ—В–Є–Ї–Є.
–Э–∞–Ј–≤–∞–љ–Є–µ –Ї—А–Є–≤–∞—П –њ–Њ–ї—Г—З–Є–ї–∞ –Ј–∞ —Б—Е–Њ–і—Б—В–≤–Њ —Б –≥—А–µ—З–µ—Б–Ї–Њ–є –±—Г–Ї–≤–Њ–є ќФ. –Х—С —Б–≤–Њ–є—Б—В–≤–∞ –≤–њ–µ—А–≤—Л–µ –Є–Ј—Г—З–∞–ї–Є—Б—М –Ы. –≠–є–ї–µ—А–Њ–Љ –≤ XVIII –≤–µ–Ї–µ, –∞ –Ј–∞—В–µ–Љ –ѓ. –®—В–µ–є–љ–µ—А–Њ–Љ –≤ XIX.
–£—А–∞–≤–љ–µ–љ–Є—П
![]() –Ф–µ–ї—М—В–Њ–Є–і–∞ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–∞ –Ї—А–∞—Б–љ—Л–Љ —Ж–≤–µ—В–Њ–Љ.
–Ф–µ–ї—М—В–Њ–Є–і–∞ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–∞ –Ї—А–∞—Б–љ—Л–Љ —Ж–≤–µ—В–Њ–Љ.


–≥–і–µ a вАФ —А–∞–і–Є—Г—Б –Ї–∞—В—П—Й–µ–≥–Њ—Б—П –Ї—А—Г–≥–∞, b вАФ —А–∞–і–Є—Г—Б –±–Њ–ї—М—И–µ–≥–Њ –Ї—А—Г–≥–∞, –њ–Њ –Ї–Њ—В–Њ—А–Њ–Љ—Г –Ї–∞—В–Є—В—Б—П –≤—Л—И–µ—Г–њ–Њ–Љ—П–љ—Г—В—Л–є –Ї—А—Г–≥. (–Э–∞ —А–Є—Б—Г–љ–Ї–µ –≤—Л—И–µ b = 3a.)
- –Т –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –Њ–љ–Њ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
 .
.

- –Я–∞—А–∞–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–µ:
 , –≥–і–µ
, –≥–і–µ  вАФ —В—А–µ—В—М –њ–Њ–ї—П—А–љ–Њ–≥–Њ —Г–≥–ї–∞.
вАФ —В—А–µ—В—М –њ–Њ–ї—П—А–љ–Њ–≥–Њ —Г–≥–ї–∞.

–°–≤–Њ–є—Б—В–≤–∞

- –Ъ—А–Є–≤–∞—П –Є–Љ–µ–µ—В —В—А–Є –Њ—Б–Њ–±–µ–љ–љ–Њ—Б—В–Є (–Ї–∞—Б–њ–∞) —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–µ
 –≤ –њ–∞—А–∞–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–Љ —Г—А–∞–≤–љ–µ–љ–Є–Є –≤—Л—И–µ.
–≤ –њ–∞—А–∞–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–Љ —Г—А–∞–≤–љ–µ–љ–Є–Є –≤—Л—И–µ.
- 3 –≤–µ—А—И–Є–љ—Л –і–µ–ї—М—В–Њ–Є–і—Л вАФ —Н—В–Њ 3 –≤–µ—А—И–Є–љ—Л —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
- –Ф–µ–ї—М—В–Њ–Є–і–∞ —П–≤–ї—П–µ—В—Б—П —А–∞—Ж–Є–Њ–љ–∞–ї—М–љ–Њ–є –Ї—А–Є–≤–Њ–є –љ—Г–ї–µ–≤–Њ–≥–Њ —А–Њ–і–∞.
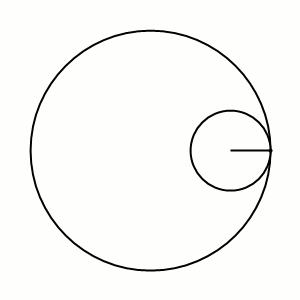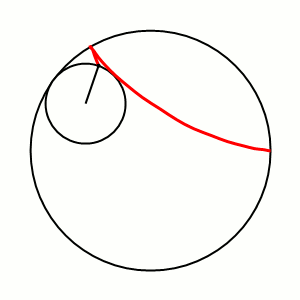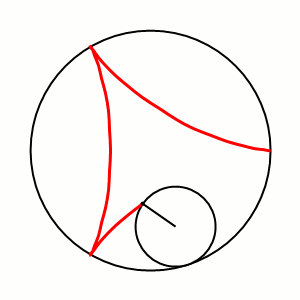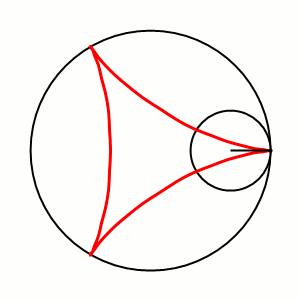
- –Ф–ї–Є–љ–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –Њ–±–ї–∞—Б—В–Є, –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–є –і–µ–ї—М—В–Њ–Є–і–Њ–є, —Б –ї—О–±–Њ–є –µ—С –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є —Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–∞ –Є —А–∞–≤–љ–∞
 , –≥–і–µ
, –≥–і–µ  вАФ —А–∞–і–Є—Г—Б –љ–µ–њ–Њ–і–≤–Є–ґ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
вАФ —А–∞–і–Є—Г—Б –љ–µ–њ–Њ–і–≤–Є–ґ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
- –Ф–µ–ї—М—В–Њ–Є–і–∞ вАФ –∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–∞—П –Ї—А–Є–≤–∞—П 4 –њ–Њ—А—П–і–Ї–∞.
- –Ф–ї–Є–љ–∞ –Ї—А–Є–≤–Њ–є
 , –≥–і–µ
, –≥–і–µ  вАФ —А–∞–і–Є—Г—Б –љ–µ–њ–Њ–і–≤–Є–ґ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
вАФ —А–∞–і–Є—Г—Б –љ–µ–њ–Њ–і–≤–Є–ґ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
- –Я–ї–Њ—Й–∞–і—М, –Њ–≥—А–∞–љ–Є—З–Є–≤–∞–µ–Љ–∞—П –і–µ–ї—М—В–Њ–Є–і–Њ–є,
 .
.
- –Ъ–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –і–≤—Г–Љ –≤–µ—В–≤—П–Љ –і–µ–ї—М—В–Њ–Є–і—Л (–љ–∞ —А–Є—Б—Г–љ–Ї–µ –≤—Б–µ —В—А–Є –≤–µ—В–≤–Є —З—С—А–љ–Њ–≥–Њ —Ж–≤–µ—В–∞), –њ—А–Њ–≤–µ–і—С–љ–љ—Л–µ –≤ –і–≤—Г—Е —В–Њ—З–Ї–∞—Е –Ї–Њ–љ—Ж–Њ–≤ –Њ—В—А–µ–Ј–Ї–∞ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є –Ї —В—А–µ—В—М–µ–є –µ—С –≤–µ—В–≤–Є (–Є–Љ–µ–љ—Г–µ–Љ—Л—Е –і–≤—Г–Љ—П —Б–≤—П–Ј–љ—Л–Љ–Є —В–Њ—З–Ї–∞–Љ–Є, –Њ–љ–Є –љ–∞ —А–Є—Б—Г–љ–Ї–µ —Б–Є–љ–µ–≥–Њ —Ж–≤–µ—В–∞), –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤—Б–µ–≥–і–∞ –њ–Њ–і –њ—А—П–Љ—Л–Љ —Г–≥–ї–Њ–Љ (–љ–∞ —А–Є—Б—Г–љ–Ї–µ –љ–µ –њ–Њ–Ї–∞–Ј–∞–љ). –Т–µ—А—И–Є–љ–∞ —Н—В–Њ–≥–Њ –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ –≤—Б–µ–≥–і–∞ –ї–µ–ґ–Є—В –љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –Љ–∞–ї–Њ–≥–Њ –Ї—А—Г–≥–∞ (–љ–∞ —В–Њ–Љ –ґ–µ —А–Є—Б—Г–љ–Ї–µ –Љ–∞–ї—Л–є –Ї—А—Г–≥ –Ї—А–∞—Б–љ–Њ–≥–Њ —Ж–≤–µ—В–∞ –Є –Њ–њ–Є—Б–∞–љ –Ї—А–∞—Б–љ–Њ–є —В–Њ—З–Ї–Њ–є –≤ —Б–µ—А–µ–і–Є–љ–µ —Б–Є–љ–µ–≥–Њ –Њ—В—А–µ–Ј–Ї–∞), –Ї–∞—Б–∞—О—Й–µ–≥–Њ—Б—П —В—А—С—Е —Г–Ї–∞–Ј–∞–љ–љ—Л—Е –≤–µ—В–≤–µ–є[1].
–Я—А–Є–ї–Њ–ґ–µ–љ–Є—П
–Ф–µ–ї—М—В–Њ–Є–і—Л –≤–Њ–Ј–љ–Є–Ї–∞—О—В –≤ –љ–µ—Б–Ї–Њ–ї—М–Ї–Є—Е –Њ–±–ї–∞—Б—В—П—Е –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є. –Э–∞–њ—А–Є–Љ–µ—А:
–°–Љ. —В–∞–Ї–ґ–µ
–Я—А–Є–Љ–µ—З–∞–љ–Є—П
- вЖС –°–∞–≤—С–ї–Њ–≤, 1960, —Б. 127.
- вЖС Lockwood, 1961.
- вЖС Dunn, J. A., and Pretty, J. A., "Halving a triangle," Mathematical Gazette 56, May 1972, 105вАФ108.
- вЖС Area bisectors of a triangle (–љ–µ–Њ–њ—А.). –Ф–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П: 29 –Њ–Ї—В—П–±—А—П 2019. –Р—А—Е–Є–≤–Є—А–Њ–≤–∞–љ–Њ 21 –љ–Њ—П–±—А—П 2017 –≥–Њ–і–∞.
–Ы–Є—В–µ—А–∞—В—Г—А–∞