黎曼流形
|
Read other articles:

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) شيون - قرية - تقسيم إداري البلد إيران المحافظة لرستان المقاطعة أليغودرز الناحية ناحية زاز و

Chilean military officer In this Spanish name, the first or paternal surname is Arellano and the second or maternal family name is Stark. Sergio Arellano StarkArellano Stark as aide de camp for Eduardo Frei MontalvaBorn(1921-06-10)10 June 1921Santiago, ChileDied9 March 2016(2016-03-09) (aged 94)Santiago, ChileService/branch Chilean ArmyYears of service1964–1976Rank Lieutenant generalCommands heldNational Intelligence DirectorateSpouse(s)Raquel Iturriaga Sergio Arellano Sta...

The SalesmanPoster bioskopSutradara Asghar Farhadi Produser Alexandre Mallet-Guy Asghar Farhadi Ditulis oleh Asghar Farhadi PemeranShahab HosseiniTaraneh AlidoostiBabak KarimiPenata musikSattar Oraki [fa]SinematograferHossein JafarianPenyuntingHayedeh SafiyariPerusahaanproduksiMemento Films ProductionAsghar Farhadi ProductionArte France CinémaDistributorFilmiran (Iran)Memento Films Distribution (Prancis)Tanggal rilis 21 Mei 2016 (2016-05-21) (Cannes) 31 Agustus 20...

Melayu CocosPengantin Melayu dalam acara pernikahan di Kepulauan Cocos (Keeling), 1912.Daerah dengan populasi signifikan Malaysia 4.000[1] Kepulauan Cocos (Keeling) 400BahasaMelayu Cocos, Inggris, MalaysiaAgamaIslamKelompok etnik terkaitJawa, Betawi, Sunda Melayu Cocos adalah sekelompok masyarakat asli/lokal yang berbudaya Melayu yang membentuk mayoritas penduduk Kepulauan Cocos (Keeling), yang sekarang merupakan bagian wilayah/teritori dari negara Australia. Meskipun merek...

Klaus Graf (* 15. Februar 1964 in Lauffen am Neckar) ist ein deutscher Jazzsaxophonist. Inhaltsverzeichnis 1 Leben 2 Projekte 2.1 Klaus Graf Jazzquartett 2.2 Timeless Art Orchestra 2.3 Salsafuerte 3 Auszeichnungen 4 Weblinks Leben Klaus Graf inmitten der SWR Big Band (erste Reihe, dritter Musiker von links) Graf war 1985 Mitglied im Jugendjazzorchester Baden-Württemberg (unter Leitung von Jiggs Whigham und Bernd Konrad) und gewann 1986 (mit der Band Cornichon) den ersten Preis beim Jugend Ja...

Bajo alemán mediosajón medio sassesch, düdesch, neddersasseschHablantes Extinto evolucionó al bajo alemán modernoFamilia Indoeuropea Germánica Germánica occidental Bajogermánica Bajo alemán medioEscritura Latino (Fraktur)Estatus oficialOficial en Liga Hanseática Norte de Europa en 1400, mostrando la extensión de la Liga Hanseática [editar datos en Wikidata&#...

Peter, Paul and MaryPeter, Paul and Mary di Westbury Music Fair, Westbury, New York, 5 Agustus 2006.Informasi latar belakangAsalNew York City, New York, Amerika SerikatGenremusik folkTahun aktif1961-19701978-2009LabelWarner Bros. RecordsSitus webhttp://www.peterpaulandmary.comMantan anggotaPeter YarrowNoel Paul StookeyMary Travers Peter, Paul and Mary 1963 Peter, Paul and Mary (sering disingkat PP&M) adalah trio pop-folk dari Amerika Serikat yang terdiri dari Peter Yarrow, Noel Paul Stook...

Czech politician Andrea ČeškováAndrea Češková with Milan Jančík.Member of the European Parliamentfor Czech RepublicIn office14 July 2009 – 30 June 2014 Personal detailsBorn (1971-10-18) 18 October 1971 (age 52)Prague, Czech RepublicPolitical partyCivic Democratic PartyAlma materCharles University in Prague Andrea Češková (born 18 October 1971) is a Czech Civic Democratic Party politician. She was a Member of the European Parliament for the Czech Republic betwee...

2022 studio album by MarillionAn Hour Before It's DarkStudio album by MarillionReleased4 March 2022 (2022-03-04)Recorded2021Studio The Racket Club, Aylesbury, Buckinghamshire Real World, Box, Wiltshire Ace, Aartselaar, Belgium GenreNeo-progressive rockLength54:10LabelIntactearMUSICProducerMarillionMichael HunterMarillion chronology With Friends from the Orchestra(2019) An Hour Before It's Dark(2022) Professional ratingsReview scoresSourceRatingClassic Rock[1] An...

Italian cycling team GW–Shimano–SidermecTeam informationUCI codeDRARegisteredItaly (1996–2022)Colombia (2023–)Founded1996 (1996)Discipline(s)RoadStatusUCI ProTeam (1996–2022)UCI Continental (2023–)BicyclesBottecchiaWebsiteTeam home pageKey personnelGeneral managerGianni SavioTeam name history19961997–19981999200020012002–2005200620072008–20092010–20112012–201420152016–201720172018–202120222023–Gaseosas Glacial–Selle ItaliaKross–Selle ItaliaSelle ItaliaAgua...

1997 video game 1997 video gameThe City of Lost ChildrenDeveloper(s)PsygnosisPublisher(s)PsygnosisJP: GameBankDirector(s)Denis FriedmanProducer(s)Carole FaureWriter(s)Nicolas MeylaenderComposer(s)Francis GorgéPlatform(s)MS-DOSPlayStationReleaseMS-DOSNA: 2 April 1997[1]EU: 1997PlayStationNA: 31 May 1997EU: 1 June 1997JP: 15 January 1998[2]Genre(s)AdventureMode(s)Single-player The City of Lost Children[a] is an adventure game developed and published by Psygnosis in 1997...

Les règles de composition en peinture occidentale sont un ensemble de techniques qui varient suivant les peintres, les styles, les mouvements et les époques et qui peuvent être aussi mélangées. Un exemple de grande composition dans un plafond de Tiepolo : tous les personnages sont placés sur des cercles et des ellipses qui se resserrent vers le soleil et Apollon, au centre. Art des diagonales La Flagellation du Christ, de Piero della Francesca, est un exemple d'utilisation du recta...
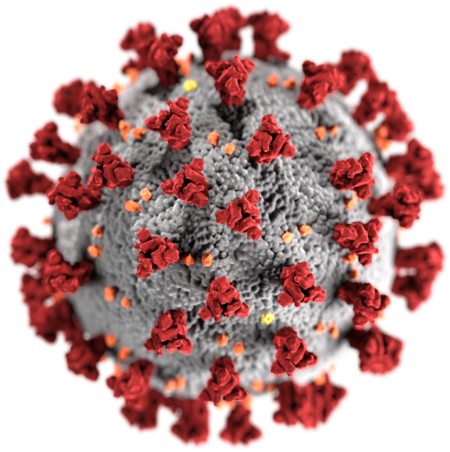
Bagian dari seri artikel mengenaiPandemi Covid-19Permodelan atomik akurat yang menggambarkan struktur luar virus SARS-CoV-2. Tiap bola yang tergambarkan di sini adalah sebuah atom. SARS-CoV-2 (virus) Covid-19 (penyakit) Kronologi2019 2020 Januari Februari Maret April Mei Juni Juli Agustus September Oktober November Desember 2021 Januari Februari Maret April Mei Juni Juli Agustus September Lokasi Menurut benua Afrika Antarktika Asia Eropa Amerika Selatan Amerika Utara Oseania Menurut kendaraan...

Sporting event delegationMorocco at the2024 Summer ParalympicsFlag of MoroccoIPC codeMARNPCRoyal Moroccan Federation of Sports for Disabledin Paris, FranceAugust 28, 2024 (2024-08-28) – September 8, 2024 (2024-09-08)Competitors22 in 4 sportsSummer Paralympics appearances (overview)1988199219962000200420082012201620202024 Morocco is scheduled to compete at the 2024 Summer Paralympics in Paris, France from 28 August to 8 September. Competitors The following ...

Carl David AndersonCarl Anderson di LNLB, Amerika Serikat tahun 1937Lahir(1905-09-03)3 September 1905New York City, New York, Amerika SerikatMeninggal11 Januari 1991(1991-01-11) (umur 85)San Marino, California, Amerika SerikatKebangsaanAmerika SerikatAlmamaterInstitut Teknologi CaliforniaDikenal atasPenemuan positronPenemuan muonPenghargaanPenghargaan Nobel dalam Fisika (1936) Medali Elliott Cresson (1937)Karier ilmiahBidangFisikaMahasiswa ternamaDonald A. GlaserSeth Neddermeyer Untuk ak...

Obliquus capitis inferior muscleDeep muscles of the back. (Obliq. infer. labeled at upper left.)DetailsOriginspinous process of the axisInsertionlateral mass of atlasNervesuboccipital nerveActionsRotation of head and neckIdentifiersLatinmusculus obliquus capitis inferiorTA98A04.2.02.007TA22252FMA32528Anatomical terms of muscle[edit on Wikidata] The obliquus capitis inferior muscle (/əˈblaɪkwəs ˈkæpɪtɪs/) is a muscle in the upper back of the neck. It is one of the suboccipital musc...

Scottish moving and warehousing company Shore Porters SocietyFounded1498; 525 years ago (1498)HeadquartersAberdeen, ScotlandServicesHaulage, removals and storageWebsitewww.shoreporters.com The Shore Porters Society is a removals, haulage and storage company based in Aberdeen, Scotland, established by minute of the local council dated 22 June 1498.[1][2] The company originated as a group or co-operative of porters working in Aberdeen Harbour. In 1666 ,two trad...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Astro Kirana – berita · surat kabar · buku · cendekiawan · JSTOR Astro KiranaLogo Astro KiranaDiluncurkan1 Juni 2006Ditutup20 Oktober 2008JaringanFirst MediaPemilikLippo GroupFormat gambar576i SDTVSlogan...

Sweet Indonesian rice dessert LupisTriangle-shaped Lupis unwrapped and sprinkled with coconut flakes served after being set in coconut sugar syrup.Alternative namesLopisTypeKueCourseDessertPlace of originIndonesiaRegion or stateSoutheast AsiaMain ingredientsGlutinous rice, coconut, palm sugar syrupOther informationPronounced lu:pɪs Lupis (sometimes lopis) is an Indonesian traditional sweet cake made of glutinous rice, banana leaves, coconut, and brown sugar sauce.[1] Lupis is one of ...

Flowering plant genus in the Acanthaceae Acanthus Acanthus montanus Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Asterids Order: Lamiales Family: Acanthaceae Subfamily: Acanthoideae Tribe: Acantheae Genus: AcanthusL. Species See text Synonyms Cheilopsis Moq.[1] Acanthus is a genus of about 30 species of flowering plants in the family Acanthaceae, native to tropical and warm temperate regions, with the highest species diversi...
