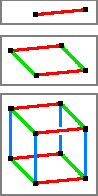
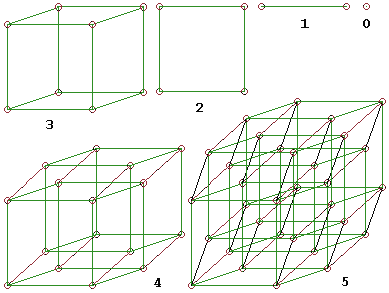
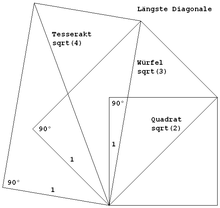
Hyperwürfel
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Indian television channel Television channel Zee BanglaCountryIndiaBroadcast areaIndiaBangladeshHeadquartersKolkata, West Bengal, IndiaProgrammingLanguage(s)BengaliOwnershipOwnerZee Entertainment EnterprisesSister channelsZee ChannelsHistoryLaunched15 September 1999FounderSubhash ChandraFormer namesAlpha TV Bangla (1999–2005)LinksWebsiteZee Bangla on ZEE5 Zee Bangla is an Indian Bengali language general entertainment pay television channel owned by the Zee Entertainment Enterprises. History...

Untuk tim sepak bola yang berbasis di Dorset, lihat Gillingham Town F.C. GillinghamNama lengkapGillingham Football ClubJulukanThe GillsBerdiri1893 (1893) (sebagai New Brompton)StadionStadion Priestfield, Gillingham, Kent(Kapasitas: 11,582)KetuaPaul ScallyManajerMartin AllenLigaLiga Satu Inggris2012-13ke-1, Liga Dua Inggris(promosi)Situs webSitus web resmi klub Kostum kandang Kostum tandang Musim ini Gillingham Football Club adalah sebuah klub sepak bola profesional asal Inggris yang...

Тотілалат. Totilaгрец. Τωτίλας Народився 510 або 510[1]Тревізо, Венето, ІталіяПомер 552[2]Гуальдо-Тадіно, Провінція Перуджа, Умбрія, Італія·загибель у битвіКраїна Королівство остготівНаціональність остготДіяльність монархУчасник Battle of TaginaedТитул корольПосада корол...

Станіслав ОрликПомер 1559Краків, Королівство ПольськеПоховання КраківКраїна Королівство ПольськеПосада Писар великий коронний, Писар Польний Короннийd і Q100230861? У Вікіпедії є статті про інших людей із прізвищем Орлик. Станіслав Орлик гербу Новина (пол. Stanisław Orlik;...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) كاترين باول معلومات شخصية اسم الولادة (بالإنجليزية: Catherine Clare Powell) الميلاد سنة 1967 (العمر 55–56 سنة) لندن الإقامة باريس مواطنة المملكة المتح�...

Martas Rango temporal: Mioceno-Reciente PreЄ Є O S D C P T J K Pg N Martas martasTaxonomíaReino: AnimaliaFilo: ChordataSubfilo: VertebrataClase: MammaliaInfraclase: PlacentaliaOrden: CarnivoraSuborden: CaniformiaFamilia: MustelidaeSubfamilia: GuloninaeGénero: MartesPinel, 1792Especies Véase texto [editar datos en Wikidata] Martas es un género de mamíferos carnívoros de la familia de los mustélidos, que incluye las martas y la garduña. Se distribuyen por Eurasia y el...

CityIlópolisCity FlagSealNickname: The Yerba Tea CityPopulation (2020 [1]) • Total4,066Time zoneUTC−3 (BRT)ZIP code95990-000 Ilópolis is a municipality in the state of Rio Grande do Sul, Brazil. History At the beginning of the twentieth century came the colony of Itapuca, founded by the Government of the State. In 1905 began on colonization of the current City of Ilópolis, with the arrival of immigrants. When in 1915, was the City of Encantado, their lan...

DistanceSutradara Hirokazu Koreeda Produser Masayuki Akieda Ditulis oleh Hirokazu Koreeda PemeranArata Yusuke IseyaSusumu TerajimaYui NatsukawaSinematograferYutaka YamasakiPenyuntingHirokazu KoreedaTanggal rilis10 Mei 2001 (2001-05-10)(France)26 Mei 2001 (2001-05-26)Durasi132 menitNegara Jepang Bahasa Jepang Distance adalah film Jepang tahun 2001 yang disutradarai oleh Koreeda Hirokazu dan dibintangi oleh Arata, Tadanobu Asano, Iseya Yusuke, Terajima Susumu, dan Natsukawa Yui. Pemer...

Halaman ini berisi artikel tentang cerita E. T. A. Hoffmann. Untuk balet, lihat The Nutcracker. Ilustrasi dari edisi AS tahun 1853 Berbagai boneka pemecah kacang tradisional Boneka Pemecah Kacang dan Raja Tikus (Jerman: Nussknacker und Mausekönig) adalah sebuah cerpen yang ditulis pada tahun 1816 oleh pengarang Jerman E. T. A. Hoffmann, dimana mainan Natal kesukaan Marie Stahlbaum, boneka pemecah kacang, menjadi hidup dan, setelah mengalahkan Raja Tikus jahat dalam pertempuran, mengajakn...

Израильско-суринамские отношения Израиль Суринам Медиафайлы на Викискладе Израильско-суринамские отношения — настоящие и исторические международные дипломатические, политические, экономические, военные, культурные и прочие отношения между Государством Израи�...

U.S. House district for California CA-51 redirects here. For California State Route 51, see Interstate 80 Business (Sacramento, California). California's 51st congressional districtInteractive map of district boundaries since 2023 (Used in the 2022 elections)Representative Sara JacobsD–San DiegoArea4,896 sq mi (12,680 km2)Population (2022)757,528[1]Median householdincome$100,357[2]Ethnicity69.4% Hispanic13.3% White8.3% Asian6.7% Black1.5% Two or more rac...

Municipality in Rhineland-Palatinate, GermanyBrimingen Municipality Coat of armsLocation of Brimingen within Eifelkreis Bitburg-Prüm district Brimingen Show map of GermanyBrimingen Show map of Rhineland-PalatinateCoordinates: 49°58′12″N 06°21′54″E / 49.97000°N 6.36500°E / 49.97000; 6.36500CountryGermanyStateRhineland-PalatinateDistrictEifelkreis Bitburg-Prüm Municipal assoc.Bitburger LandGovernment • Mayor (2018–24) Peter NeysesArea ...

2015 single by Duke DumontThe Giver (Reprise)Single by Duke DumontReleased14 June 2015Recorded2012GenreDeep houseLength3:23LabelTurboSongwriter(s)Adam DymentByron StingilyHal RitsonByron BurkeKelli-Leigh Henry-DavilaProducer(s)Duke DumontDuke Dumont singles chronology Won't Look Back (2014) The Giver (Reprise) (2015) Ocean Drive (2015) The Giver (Reprise) is a vocal remix of the 2012 song The Giver by British DJ and record producer Duke Dumont. It was released as a digital download in the Uni...

Iglesia Nuestra Señora de Lourdes y San Vicente Pallotti Monumento Histórico Nacional LocalizaciónPaís UruguayDivisión MontevideoCoordenadas 34°54′11″S 56°12′02″O / -34.903069, -56.200674Información religiosaCulto catolicismoHistoria del edificioFundación 1888Arquitecto Ignacio PedralbesDatos arquitectónicosEstilo neobarroco[editar datos en Wikidata] Interior de la Iglesia en 1946, fotografía por el Centro de Fotografía de Montevideo. La Iglesia d...

Este artículo se refiere o está relacionado con una infraestructura de transporte público futura o en desarrollo. La información de este artículo puede cambiar frecuentemente. Por favor, no agregues datos especulativos y recuerda colocar referencias a fuentes fiables para dar más detalles. Autopista Dos Mares España España Datos de la rutaIdentificador Tipo AutopistaLongitud 111,4 kmAdministraciónAdministración OrientaciónInicio Pesquera (Cantabria)Fin Miranda de E...

2010 single by Yolanda Be Cool and DCUP We No Speak AmericanoSingle by Yolanda Be Cool and DCUPReleased27 February 2010Recorded2008GenreElectro swing[1][2]house[3]Length4:29 (original version)2:58 (radio edit)2:11 (UK radio edit)LabelSweat It Out!Songwriter(s)Johnson PetersonSylvester MartinezDuncan MaclennanRenato CarosoneNicola SalernoProducer(s)Yolanda Be CoolDCUPYolanda Be Cool singles chronology Holy Cow (2009) We No Speak Americano (2010) Le Bump (2011) We No...

Saraswati Education SocietyTypeEducational SocietyEstablished2003PresidentDr. Nandkumar Y. TasgaonkarLocationKarjat, Maharashtra, IndiaCampusRuralWebsitetasgaonkartech.com Saraswati Education Society is an Indian public charitable trust which was formed on 10 October 2003 by Dr Nandkumar Y. Tasgaonkar, who serves as its chairman. Since its inception, the trust has established ten institutions at Bhivpuri Road station, Karjat, Raigad district, Maharashtra, which provide professional courses in...

1980 Japanese filmTora-san's Tropical FeverTheatrical posterDirected byYoji YamadaWritten byYoji YamadaYoshitaka AsamaStarringKiyoshi AtsumiRuriko AsaokaCinematographyTetsuo TakabaEdited byIwao IshiiMusic byNaozumi YamamotoDistributed byShochikuRelease date August 2, 1980 (1980-08-02) Running time104 minutesCountryJapanLanguageJapanese Tora-san's Tropical Fever (男はつらいよ 寅次郎ハイビスカスの花, Otoko wa Tsurai yo: Torajirō Haibisukasu no Hana)[1] a...

Kecapi, seruling dan sitar pada relief Borobudur, foto ca. 1890 Musik dari Indonesia Garis waktuContoh Jenis KlasikDaerahTradisionalJazzHip hopPopRokR&BKeroncongDangdut Bentuk khusus Jawa KidungTembangLanggamGamelanAngklungCalungCampursariTarlingMusik tegalanKecapi sulingGambangJaranan dangdut Bali GenggongRindikCeng cengGuntangGamelan BaliKecak Sumatra Zapin Kalimantan SapehKatambungSampe Sulawesi Kolintang Nusa Tenggara Timur Sasando Maluku TifaKulintang Papua TritonFuuTifaKrambiP...

For other uses, see Defying Gravity (disambiguation). 1997 American filmDefying GravityDirected byJohn KeitelWritten byJohn KeitelProduced byJack KollDavid Clayton MillerStarring Daniel Chilson Niklaus Lange Don Handfield Linna Carter CinematographyTom HartingEdited byMatthew YagleDistributed byWolfe VideoRelease date1997Running time92 minutesCountryUnited StatesLanguageEnglish Defying Gravity is a 1997 independent gay-themed romantic drama directed by John Keitel and starring Daniel Chilson,...