Coherent space
|
Read other articles:

Questa voce sull'argomento calciatori russi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Igor' Leščuk Nazionalità Russia Altezza 187 cm Peso 83 kg Calcio Ruolo portiere Squadra Dinamo Mosca Carriera Giovanili Dinamo Mosca Squadre di club1 2016- Dinamo-2 Mosca11 (-14)2016- Dinamo Mosca1 (0) Nazionale 2010 Russia U-152 (0)2010-2011 Russia U-164 (0)2016 Russia U-215 (0) Pa...

معركة بوياكا يُشير إعلان استقلال كولومبيا إلى الأحداث التي وقعت في 20 يوليو 1810؛ في «سانتا في دي بوغوتا»، في النيابة الملكية الاستعمارية الإسبانية لغرناطة الجديدة. وقد نتج عن تلك الأحداث في ذلك اليوم؛ إنشاء «الخونتا العسكرية لسانتا في». وقد أدت تجربة الحكم الذاتي في نهاية ا�...

PapercutSingel oleh Linkin Parkdari album Hybrid TheorySisi-B Points of Authority (Live) Papercut (Live) Dirilis18 Juni 2001[1]DirekamLos Angeles, California, 2000Genre Nu metal[2][3] rap metal[4] Durasi3:05LabelWarner Bros.PenciptaLinkin ParkProduserDon GilmoreKronologi singel Linkin Park Crawling (2000) Papercut (2001) In the End (2001) Papercut adalah sebuah lagu oleh grup musik rok Amerika Linkin Park. Lagu ini dirilis sebagai single internasional ketiga da...

Friedrich III. von Sachsen-Gotha, Gemälde von Christian Schilbach, 1720 Herzog Friedrich III. von Sachsen-Gotha-Altenburg Friedrich III. von Sachsen-Gotha-Altenburg (* 14. Apriljul. / 24. April 1699greg. in Gotha; † 10. März 1772 ebenda) war ein Fürst aus der Nebenlinie Sachsen-Gotha-Altenburg der Ernestinischen Wettiner und von 1732 bis 1772 Herzog von Sachsen-Gotha-Altenburg. Inhaltsverzeichnis 1 Leben 2 Sonstiges 3 Ehe und Nachkommen 4 Literatur 5 Weblinks 6 Einzel...

Norwegian footballer (born 1972) Vidar Riseth Riseth pictured in 2006Personal informationFull name Vidar Riseth[1]Date of birth (1972-04-21) 21 April 1972 (age 51)[2]Place of birth Frosta, NorwayHeight 1.89 m (6 ft 2 in)[3]Position(s) Centre-back, midfielderYouth career0000–1990 Neset1991–1992 RosenborgSenior career*Years Team Apps (Gls)1992–1993 Rosenborg 11 (2)1993–1996 Kongsvinger 56 (20)1995–1996 → Luton Town (loan) 11 (0)1996–1998...

Kirab Pusakaꦏꦶꦫꦧ꧀ꦥꦸꦱꦏKirab Pusaka di area kotaStatusAktifJenisFestival budayaFrekuensiTahunanLokasiPonorogoNegaraIndonesia Kirab Pusaka (Jawa: ꦏꦶꦫꦧ꧀ꦥꦸꦱꦏ, translit. Kirab Pusaka) adalah salah satu rangkaian acara Grebeg Suro yang rutin dilaksanakan setiap tahunnya di Ponorogo. Acara ini dilaksanakan dalam rangka memperingati tahun baru Islam yang jatuh pada tanggal 1 Muharram (1 Suro).[1] Secara historis, kirab pusaka merupakan sebuah simbol...

Artikel ini membutuhkan penyuntingan lebih lanjut mengenai tata bahasa, gaya penulisan, hubungan antarparagraf, nada penulisan, atau ejaan. Anda dapat membantu untuk menyuntingnya. Badan Pengembangan Sumber Daya Manusia Energi dan Sumber Daya Mineral Gambaran umumDibentuk2001; 21 tahun lalu (2001)Nomenklatur sebelumnyaBadan Pendidikan dan PelatihanSloganJujur, Profesional, Melayani, Inovatif, BerartiSusunan organisasiKepala BadanPrahoro Yulianto NurtjahyoSekretaris BadanIr. Wakhid Hasyim...

Traktat Gallipoli, ditandatangani pada Januari atau awal Februari 1403, adalah sebuah traktat perdamaian antara Süleyman Çelebi, penguasa wilayah Utsmaniyah di Balkan, dengan kekuatan-kekuatan regional Kristen utama: Kekaisaran Romawi Timur, Republik Venesia, Republik Genova, Ksatria Hospitaller, dan Kadipaten Naxos. Traktat ini ditandatangani setelah berakhirnya Pertempuran Ankara, ketika Süleyman berupaya memperkuat posisinya sendiri dalam perebutan suksesi dengan para saudaranya, trakta...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2017) محمد كوني (بالفرنسية: Mohamed Koné) معلومات شخصية الميلاد 24 مارس 1981 (العمر 42 سنة)أبيدجان الطول 6 قدم 11 بوصة (2.1 م) مركز اللعب لاعب هجوم قوي الجسم الجنسي

County in Oklahoma, United States County in OklahomaCreek CountyCountyCreek County Courthouse, Sapulpa in 2014Location within the U.S. state of OklahomaOklahoma's location within the U.S.Coordinates: 35°54′N 96°22′W / 35.9°N 96.37°W / 35.9; -96.37Country United StatesState OklahomaFounded1907Named forCreek NationSeatSapulpaLargest citySapulpaArea • Total970 sq mi (2,500 km2) • Land950 sq mi (2,500 ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2016. Trio JulitTrio JulitInformasi latar belakangAsalJakarta, IndonesiaGenreDangdutPopTahun aktif2015 - sekaranArtis terkaitBintang PanturaAnggotaRamziIrfan HakimAndhika Pratama Trio Julit merupakan sebuah grup yang beranggotakan para host ajang Bintang Pantu...

село Солошине Герб Країна Україна Область Полтавська область Район Кременчуцький район Громада Горішньоплавнівська міська громада Основні дані Населення 836 Поштовий індекс 39245 Телефонний код +380 5343 Географічні дані Географічні координати 48°57′12″ пн. ш. 33°56′44″...
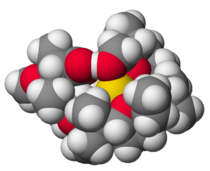
Seperti kebanyakan antibiotik, monensin-A adalah suatu ionofor yang secara kuat mengikat Na+ (ditunjukkan dalam warna kuning).[1] Kimia bioanorganik adalah suatu bidang yang meneliti peran logam dalam biologi. Bioanorganik kimia meliputi studi baik dari fenomena alam seperti perilaku metaloprotein serta logam buatan yang diperkenalkan, termasuk mereka yang non-esensial, dalam bidang kedokteran dan toksikologi. Banyak proses biologis seperti respirasi bergantung pada molekul yang berad...

2005 single by DJ Tomekk This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Jump, Jump – news · newspapers · books · scholar · JSTOR (November 2015)Jump, JumpSingle by DJ Tomekk featuring Fler and G-Hotfrom the album Numma Eyns Released2005GenreHip HopLength3:05Songwriter(s)Freddie PerrenBerry GordyJe...

Road on Howth Head, Dublin Carrickbrack RoadR105Housing off Carrickbrack RoadNative nameBóthar Charraig Bhreac (Irish)NamesakeCarrickbrack RockLength4.5 km (2.8 mi)Width11 metres (36 ft)LocationHowth Head, Dublin, IrelandPostal codeD13Coordinates53°22′19″N 6°05′15″W / 53.371816°N 6.087629°W / 53.371816; -6.087629west endGreenfield Roadeast endThormanby Road Carrickbrack Road (Irish: Bóthar Charraig Bhreac)[1] is a roa...

Bahasa Ping 平话 / 平話 Pinghua Bahasa Ping ditulis dalam aksara HanDituturkan diTiongkokWilayahGuangxi dan HunanPenutursekitar 7 juta jiwa (2016)[1]Rumpun bahasaSino-Tibet SinitikTionghoaPing DialekPing Utara Ping Selatan Kode bahasaISO 639-3Mencakup:csp – Southern Ping Chinesecnp – Northern Ping ChineseGlottologping1245Linguasfer79-AAA-oLokasi penuturanPeta bahasa lainInformasi tambahan Pinghua Hanzi tradisional: 平話 Hanzi sederhana: 平话 A...

Privileged social class in Switzerland This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may need to be rewritten to comply with Wikipedia's quality standards. You can help. The talk page may contain suggestions. (November 2011) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material ...

Japanese baseball player Baseball player Shoma SatoChiba Lotte Marines – No. 64PitcherBorn: (1998-06-02) June 2, 1998 (age 25)Sumida, Tokyo, JapanBats: LeftThrows: LeftNPB debutMarch 31, 2022, for the Chiba Lotte MarinesCareer statistics (through 2022 season)Win-loss record2-6Earned run average4.64Strikeouts28Holds0Saves0 Teams Chiba Lotte Marines (2022-present) Shoma Sato (佐藤 奨真, Sato Shoma, born June 2, 1998 in Sumida, Tokyo, Japan) is a professional Japanese b...

Radio station in Centerville, IowaKCOGCenterville, IowaBroadcast areaAppanoose County, IowaFrequency1400 kHzBrandingCenterville's True Oldies ChannelProgrammingFormatTrue OldiesAffiliationsAccuWeatherFox News RadioFox Sports RadioOwnershipOwnerEdwin BrandHoney Creek Broadcasting, LLCSister stationsKMGOHistoryFirst air dateFebruary 27, 1949Call sign meaningKeep Calling On GodTechnical informationFacility ID33736ClassCPower500 watts day1000 watts nightTranslator(s)103.9 K280GY (Centerville...

The Twilight Saga: The Official Illustrated Guide AuthorStephenie MeyerOriginal titleThe Twilight Saga: The Official GuideCountryUnited StatesLanguageEnglishSeriesThe Twilight SagaGenreFantasyPublisherLittle, BrownPublication dateApril 12, 2011[1]Media typePrint (Hardcover, Paperback) e-Book (Kindle)Pages576[1]ISBN978-0-316-04312-0 The Twilight Saga: The Official Illustrated Guide (previously titled The Official Guide) is a spin-off encyclopedic reference book for th...




























