Stratifold
|
Read other articles:

The TreePoster filmSutradara Sonja Prosenc ProduserDitulis oleh Sonja Prosenc PemeranKatarina StegnarTanggal rilis 7 Juli 2014 (2014-07-07) (Karlovy) Durasi90 menitNegara Slovenia Bahasa Slovenia The Tree (bahasa Slovenia: Drevo) adalah sebuah film drama Slovenia 2014 yang ditulis dan disutradarai oleh Sonja Prosenc. Film tersebut terpilih menjadi perwakilan Slovenia untuk Film Berbahasa Asing Terbaik di Academy Awards ke-88 namun tidak masuk nominasi.[1][2] Pemeran …

العلاقات الأسترالية الصربية أستراليا صربيا أستراليا صربيا تعديل مصدري - تعديل العلاقات الأسترالية الصربية هي العلاقات الثنائية التي تجمع بين أستراليا وصربيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة

Cruise ship Emerald Princess Emerald Princess near Hook of Holland, 2020 History Bermuda NameEmerald Princess Owner Carnival Corporation & plc OperatorPrincess Cruises Port of registryHamilton, Bermuda Ordered23 September 2004 BuilderFincantieri, Italy CostUS$500 million Laid down14 September 2005 Launched1 June 2006[1] Christened13 May 2007 by Florence Henderson, Marion Ross, Erin Moran and Susan Olsen Acquired24 March 2007 Maiden voyage11 April 2007 Identification Call sign: …

Area of Stamford in Connecticut, US 41°03′22″N 73°31′17″W / 41.0561°N 73.5213°W / 41.0561; -73.5213 NeighborhoodEast SideNeighborhoodThe headquarters of NBC SportsEast SideCoordinates: 41°03′22″N 73°31′17″W / 41.0561°N 73.5213°W / 41.0561; -73.5213Area • Total2.2 km2 (0.84 sq mi)Population (2015-2019) • Total8,181 • Density3,800/km2 (9,700/sq mi) William Street Sch…
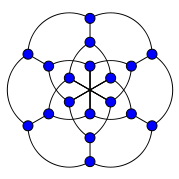
Граф Паппа В Теорії графів графом Паппа називається двочастковий кубічний (або 3-регулярний) неорієнтований граф з 18 вершинами і 27 ребрами, є графом Леві конфігурації Паппа. Він названий на честь Паппа Олександрійського, математика Стародавньої Греції, який вірив, що довів…

Oblystar du Kazakhstan Le Kazakhstan est divisé en 17 provinces (en kazakh облыстар (oblystar), au singulier облыс (oblys) ; en russe области (oblasti), au singulier область (oblast'))[1]. Elles étaient au nombre de 14 avant une réforme territoriale mise en œuvre en 2022. Les provinces sont subdivisées en districts (en kazakh аудандар (aýdandar), au singulier аудан (aýdan) ; en russe районы (raïoni), au singulier район (ra

1947 Texas Longhorns baseballSWC championsNCAA Western playoffConferenceSouthwest ConferenceRecord22–4 (12–3 SWC)Head coachBibb Falk (5th year)Home stadiumClark FieldSeasons← 19461948 → 1947 Southwest Conference baseball standings vte Conf Overall Team W L PCT W L PCT Texas †y 14 – 1 .933 20 – 4 .833 Baylor 9 – 5 .643 12 – 8 …

Фредерік Наттер ЧейзенНародився 1896[1][2]Саффолк, Англія, Сполучене КоролівствоПомер 13 лютого 1942(1942-02-13)[1]СінгапурКраїна Велика БританіяДіяльність зоолог, орнітолог, ботанікПосада директор музеюdДіти Гізер Чейзенd Систематик живої природи Дослідник, як

President of the Legislative Yuan立法院院長Seal of the Legislative YuanIncumbentYu Shyi-kunsince 1 February 2020Legislative YuanStyleMr President (within Legislative Yuan)SeatZhongzheng District, TaipeiAppointerLegislative YuanTerm length4 years; renewableConstituting instrumentArticle 66 of the Constitution of the Republic of ChinaFormation8 October 1928; 95 years ago (1928-10-08) (original) 17 May 1948; 75 years ago (1948-05-17) (1947 Constitution)…

AstiLogo ACD AstiNama lengkapAssociazione Calcio Dilettantistica AstiJulukanGalletti (Ayam jantan)Berdiri1932StadionStadio Cesin Bosia,Asti, Italy(Kapasitas: 6,000)KetuaGianmaria PiacenzaManajerEnrico PasqualiLigaSerie D/A2011–12Serie D/A, 15thSitus webSitus web resmi klub Kostum kandang Kostum tandang Associazione Calcio Dilettantistica Asti adalah sebuah klub sepak bola Italia dari kota Asti. Klub ini didirikan pada tahun 1932 dengan nama B.C. Asti, dan telah berganti nama beberapa kali…

Sōsuke IkematsuLahir9 Juli 1990 (umur 33)Fukuoka, Fukuoka, JepangPekerjaanPemeranTahun aktif2001–kiniAgenHoriproDikenal atasThe Last SamuraiTinggi172 m (564 ft 3+1⁄2 in)Situs webHoripro Sōsuke Ikematsu (池松 壮亮code: ja is deprecated , Ikematsu Sōsuke) (lahir 9 Juli 1990) adalah seorang pemeran televisi dan teater asal Jepang. Ia dikenal karena berperan sebagai Higen, keponakan muda dari pemimpin samurai Katsumoto, dalam film tahun 2003 The Last Samurai. …

Boulangerie : le lieu de vente. L'atelier artisanal. Une boulangerie est un type de commerce de détail de fabrication et de vente de pain, et qui propose éventuellement une gamme d'autres produits alimentaires (pâtisserie, viennoiserie, sandwichs, chocolat, confiserie, produits secs...). Elle est tenue par un boulanger et ses apprentis. Cette activité a été l'objet de bien des attentions de la part des gouvernés et gouvernants du fait de son importance dans l'alimentation. Son évolu…

Region of California in the United StatesEastern CaliforniaRegion of CaliforniaDowntown San Bernardino, anchor of the largest metro area in East California and 12th in the United States.Counties on California's Eastern BorderCountryUnited StatesStateCaliforniaTime zonePacific Standard Time • Summer (DST)Pacific Daylight TimeArea codes530, 442/760, 909, 951 Eastern California is a region defined as either the strip to the east of the crest of the Sierra Nevada or as the easternmost co…

Escola de Filosofia, Letras e Ciências Humanas Escola de Filosofia, Letras e Ciências Humanas da Universidade Federal de São Paulo EFLCH Tipo de instituição Pública Localização Guarulhos, São Paulo, Brasil Diretor(a) Magali Aparecida Silvestre Vice-diretor(a) Janes Jorge Graduação 2974 Pós-graduação 680 Página oficial unifesp.br/campus/gua Parede na EFLCH - Escola de Filosofia, Letras e Ciências Humanas. Unifesp Campus Guarulhos Interior do prédio central do Campus Guarulh…

1993 studio album by StingTen Summoner's TalesStudio album by StingReleased9 March 1993[1]RecordedJune–December 1992StudioLake House, Wiltshire, EnglandGenre Pop rock soft rock jazz rock Length52:31Label A&M PolyGram (Hong Kong) ProducerSting, Hugh PadghamSting chronology The Soul Cages(1991) Ten Summoner's Tales(1993) Fields of Gold: The Best of Sting 1984–1994(1994) Singles from Ten Summoner's Tales It's Probably MeReleased: 23 June 1992[2] If I Ever Lose My Fai…

Nigerian military officer (1940–1976) Buka Suka DimkaBirth nameBuka Suka DimkaBorn1940British NigeriaDied15 May 1976(1976-05-15) (aged 35–36)Lagos, NigeriaAllegiance NigeriaService/branch Nigerian ArmyYears of service1963–1976Rank Lieutenant Colonel Lieutenant Colonel Buka (Bukar) Suka (Suwa) Dimka (1940 – 15 May 1976)[1] was a Nigerian Army officer who played a leading role in the 13 February 1976 abortive military coup against the government of General Murtala Ra…

Comité Olímpico Argelinoاللجنة الأولمبية و الرياضية الجزائريةComité Olympique et Sportif Algérien Acrónimo COATipo Comité Olímpico NacionalFundación 1963Sede central Ben Aknoun (Argelia)Presidente Mustapha BerrafMiembro de Comité Olímpico InternacionalAsociación de Comités Olímpicos Nacionales de ÁfricaSitio web http://www.coalgerie.com/[editar datos en Wikidata] El Comité Olímpico Argelino (en árabe: اللجنة الأولمبية و …

American Licorice CompanyTypePrivateIndustryFoodFounded1914[1]HeadquartersLa Porte, Indiana, U.S.Websitewww.americanlicorice.com American Licorice Company is an American candy manufacturer founded in Chicago, Illinois in 1914, and headquartered in La Porte, Indiana.[2][3] The company has manufacturing facilities in Union City, California and La Porte.[1] History In 1925, the company began West operations in San Francisco, California.[4] That same year, it …

Indian politician (1942–2019) Sudini Jaipal ReddyJaipal Reddy in 2007Minister of Earth SciencesIn office19 October 2012 – 18 May 2014Prime MinisterManmohan SinghPreceded byVayalar RaviSucceeded byJitendra SinghMinister of Science and TechnologyIn office29 October 2012 – 18 May 2014Prime MinisterManmohan SinghPreceded byVayalar RaviSucceeded byJitendra SinghMinister of Information and BroadcastingIn office01 May 1997 – 19 March 1998Preceded byC. M. IbrahimSuccee…

Motor vehicle Subaru Crosstrek/XV2018 Subaru XVOverviewManufacturerSubaruAlso calledSubaru XV (global markets, 2012–2022)Subaru XV Crosstrek (United States and Canada, 2013–2015)Production2012–presentModel years2013–presentBody and chassisClassSubcompact crossover SUV[1]Body style5-door SUVLayoutFront-engine, all-wheel driveFront-engine, front-wheel drive (Japan, 2022–present)RelatedSubaru ImprezaChronologyPredecessorSubaru Outback Sport (United States and Canada…
































![{\displaystyle \Omega ^{O}({\text{point}})\to \mathbb {Z} /2[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d6e9664f857ef33adcc57ccb744fb30b338329a)
![{\displaystyle \Omega ^{SO}({\text{point}})\to \mathbb {Z} [t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f4a0247897ffa822d3d4236c361b81b49820a74)




