Share to:

Penyeragaman (teori himpunan)

Dalam teori himpunan, sebuah cabang matematika, aksioma penyeragaman merupakan sebuah bentuk lemah dari aksioma pemilihan. Ini menyatakan bahwa jika $R$ adalah sebuah himpunan bagian dari $X\times Y$ , dimana $X$ dan $Y$ adalah ruang Polish, maka terdapat sebuah himpunan bagian $f$ dari $R$ yang merupakan sebuah fungsi parsial dari $X$ ke $Y$ , dan yang ranahnya (himpunan semua $x$ sehingga $f(x)$ ada) sama

\{x\in X\mid \exists y\in Y:(x,y)\in R\}

Seperti sebuah fungsi disebut sebuah fungsi penyeragaman untuk $R$ , atau sebuah penyeragaman dari $R$

Untuk melihat hubungan dengan aksioma pemilihan, amatilah bahwa $R$ dapat dianggap sebagai menghubungkan, untuk setiap unsur $X$ , sebuah himpunan bagian $Y$ . Sebuah penyeragaman $R$ kemudian ambil tepatnya satu unsur dari masing-masing himpunan bagian, setiap kali himpunan bagiannya adalah takkosong. Demikian, memungkinkan himpunan sembarang $X$ dan $Y$ (daripada ruang Polish) akan membuat aksioma penyeragaman setara dengan aksioma pemilihan.

Sebuah kelas titik ${\boldsymbol {\Gamma }}$ dikatakan memiliki sifat penyeragaman jika setiap relasi $R$ di ${\boldsymbol {\Gamma }}$ dapat diseragamkan oleh sebuah fungsi parsial di ${\boldsymbol {\Gamma }}$ . Sifat penyeragaman disiratkan oleh sifat skala, setidaknya untuk kelas titik memadai bentuk tertentu.

Ini diikuti dari teori himpunan Zermelo–Fraenkel sendiri bahwa ${\boldsymbol {\Pi }}_{1}^{1}$ dan ${\boldsymbol {\Sigma }}_{2}^{1}$ memiliki sifat penyeragaman. Ini diikuti dari keberadaan kardinal besar yang cukup bahwa

${\boldsymbol {\Pi }}_{2n+1}^{1}$ dan ${\boldsymbol {\Sigma }}_{2n+2}^{1}$ memiliki sifat penyeragaman untuk setiap bilangan asli $n$ .
Oleh karena itu, kumpulan himpunan projektif memiliki sifat penyeragaman.
Setiap relasi di $\mathrm {L} (R)$ $\mathrm {L} (R)$ dapat diseragamkan, tapi tidak diperluakan oleh sebuah fungsi di $\mathrm {L} (R)$ $\mathrm {L} (R)$ . Faktanya, $\mathrm {L} (R)$ $\mathrm {L} (R)$ tidak memiliki sifat penyeragaman (dengan setara, $\mathrm {L} (R)$ $\mathrm {L} (R)$ tidak memenuhi aksioma penyeragaman).
- (Catatan: trivialnya bahwa setiap relasi di $\mathrm {L} (R)$ dapat diseragamkan di $V$ , asumsi $\mathrm {V}$ memenuhi aksioma pemilihan. Poinnya adalah bahwa setiap relasi dapat diseragamkan dalam suatu model dalam transitif $\mathrm {V}$ di mana aksioma determinasi berlaku.)

Referensi

Moschovakis, Yiannis N. (1980). Descriptive Set Theory. North Holland. ISBN 0-444-70199-0.

Read other articles:

SMA Negeri 8 Makassar

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2016. artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan...

إميل برلينر

إميل برلينر معلومات شخصية اسم الولادة (بالألمانية: Emile Berliner)‏ الميلاد 20 مايو 1851(1851-05-20)هانوفر الوفاة 3 أغسطس 1929 (78 سنة)واشنطن العاصمة سبب الوفاة نوبة قلبية الإقامة هانوفر (1851–1870)الولايات المتحدة (1870–) مواطنة ألمانيا، الولايات المتحدة الأمريكية الأولاد هنري بيرلين�...

Ernesto Ramos Antonini

Puerto Rican politician (1898–1963) In this Spanish name, the first or paternal surname is Ramos and the second or maternal family name is Antonini. Ernesto Ramos Antonini17th Speaker of the House of Representatives of Puerto RicoIn officeJanuary 2, 1945 – January 9, 1963Preceded byFrancisco M. Susoni AbreuSucceeded bySantiago Polanco AbreuSpeaker pro tempore of the House of Representatives of Puerto RicoIn officeJanuary 2, 1945 – January 9, 1963Preceded byGuillermo Alicea C...

Ухвалення рішень в умовах визначеності

Ця стаття містить правописні, лексичні, граматичні, стилістичні або інші мовні помилки, які треба виправити. Ви можете допомогти вдосконалити цю статтю, погодивши її із чинними мовними стандартами. Визначеність — це такий стан знань, коли особа, що ухвалює рішення, зазд

Прибулець (фільм, 1979)

У Вікіпедії є статті про інші значення цього терміна: Прибулець. Прибулець Жанр фантастикакомедіямелодрамаРежисер Леонід БиковСценарист Євген ШатькоЛеонід БиковГеоргій ГречкоУ головних ролях Леонід БиковГалина ПольськихОператор Вадим ІллєнкоКомпозитор Сергій Бржес

Guanidina

Guanidina Nombre IUPAC GuanidinaGeneralFórmula molecular CH5N3IdentificadoresNúmero CAS 113-00-8[1]ChEBI 42820ChEMBL CHEMBL821ChemSpider 3400DrugBank 00536PubChem 3520UNII JU58VJ6Y3B InChIInChI=InChI=1S/CH5N3/c2-1(3)4/h(H5,2,3,4)Key: ZRALSGWEFCBTJO-UHFFFAOYSA-N Propiedades físicasMasa molar 5907 g/molPunto de fusión 323,15 K (50 °C)Valores en el SI y en condiciones estándar(25 ℃ y 1 atm), salvo que se indique lo contrario.[editar datos en Wikidata]...

Зазим'я

село Зазим'я Герб Прапор Свято-Воскресенська церква у с.Зазим'я.Свято-Воскресенська церква у с.Зазим'я. Країна Україна Область Київська область Район Броварський Громада Зазимська сільська громада Код КАТОТТГ UA32060090010046220 Основні дані Засноване 1128[1] Населення 2251(201...

NUMA1

NUMA1 Наявні структури PDBПошук ортологів: PDBe RCSB Список кодів PDB 3RO2 Ідентифікатори Символи NUMA1, NUMA, NMP-22, nuclear mitotic apparatus protein 1 Зовнішні ІД OMIM: 164009 MGI: 2443665 HomoloGene: 38150 GeneCards: NUMA1 Онтологія гена Молекулярна функція • structural molecule activity• GO:0001948, GO:0016582 protein binding• microtubule binding• protein C-terminus binding• t...

Castillo de Pals

Castillo de Pals Bien de interés culturalPatrimonio histórico de España LocalizaciónPaís España EspañaComunidad Cataluña CataluñaProvincia GeronaGeronaLocalidad PalsDatos generalesCategoría MonumentoCódigo RI-51-0006004[1]Declaración 8 de noviembre de 1988[editar datos en Wikidata] El castillo de Pals es un castillo fronterizo del siglo IX en el núcleo antiguo de Pals, en el Bajo Ampurdán. Se conserva la torre del homenaje del antiguo castillo, co...

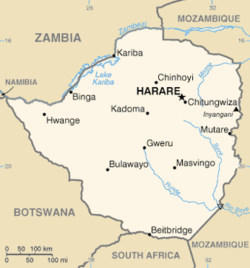
List of populated places in Zimbabwe

Map of Zimbabwe This is a list of cities, towns and villages in Zimbabwe. See also: Place names in Zimbabwe. Cities This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (September 2017) (Learn how and when to remove this template message) Harare Bulawayo Mutare Kwekwe Kadoma Cities in Zimbabwe[1] City Province Census 1982 Census 1992 Census 2002 Census 2012 Census 2022 Harare...

Schapelle Corby

Schapelle CorbyLahirSchapelle Leigh Corby10 Juli 1977 (umur 46)Tugun, Queensland, AustraliaKebangsaanAustraliaKarya terkenalMy Story;No More TomorrowsHukuman kriminal20 tahun penjaraDenda Rp 100.000.000Status kriminalBebas bersyarat 10 Februari 2014Suami/istriKimi Tanaka (nama samaran) (m. 1998; c. 2003)Orang tuaMichael Corby (wafat, 18 Januari 2008)Rosleigh RoseAlasanMengimpor marijuana atau ganja(27 Mei 2005) Schapelle Leigh Corby (la...

Гренобль

У этого термина существуют и другие значения, см. Гренобль (значения). коммунаГренобльфр. Grenoble Герб[d] Логотип 45°11′16″ с. ш. 5°43′37″ в. д.HGЯO Страна Франция Регион Овернь — Рона — Альпы Департамент Изер Мэр Эрик Пьолле История и география Площадь 18,44 км² Вы...

Guindy National Park

National park in Tamil Nadu, India Guindy National ParkIUCN category II (national park)Guindy National Park entranceLocation in Chennai, IndiaLocationChennai, Tamil Nadu, IndiaNearest cityChennaiCoordinates13°00′09″N 80°13′51″E / 13.00259°N 80.23079°E / 13.00259; 80.23079Area2.7057 km2 (1.0447 sq mi)Established1977Visitors700,000 (in 2006[1])Governing bodyTamil Nadu Forest Departmentforests.tn.nic.in Guindy National...

Alpha Delta Pi

North American collegiate sorority This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Alpha Delta Pi – news · newspapers · books · scholar · JSTOR (May 2018) (Learn how and when to remove this template message) Alpha Delta PiΑΔΠFoundedMay 15, 1851; 172 years ago (1851-05-15)Wesleyan College...

不必在乎我是誰

不必在乎我是誰林憶蓮的录音室专辑发行日期1993年5月19日类型國語流行音樂时长52:10唱片公司星工廠滾石唱片制作人許願李宗盛林憶蓮小蟲林憶蓮专辑年表不如重新開始（1993年4月29日）不如重新開始字符串模块出错：找不到匹配不必在乎我是誰（1993年5月19日） Simple（1994年3月10日）Simple字符串模块出错：找不到匹配《不必在乎我是誰》是香港歌手林憶蓮第十五張錄音室專�...

Pontificios Colegios en Roma

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada.Este aviso fue puesto el 23 de mayo de 2014. Collegio Romano (Roma), sede del Liceo Ginnasio Ennio Quirino Visconti. Los pontificios colegios en Roma son instituciones creadas por la Santa Sede, al modo de Colegios Mayores de estudiantes, para proveer la formación de seminaristas y sacerdotes, en las universidades pontificias de Roma. A la hora de su elección canónica, se suelen mirar algunos criter...

KYTV (TV series)

British television series This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: KYTV TV series – news · newspapers · books · scholar · JSTOR (February 2023) (Learn how and when to remove this template message) KYTVGenreComedyWritten byAngus DeaytonGeoffrey PerkinsDirected byJohn KilbyJohn StroudStarringHelen ...

Time Hollow

2008 video gameTime HollowDeveloper(s)TenkyPublisher(s)KonamiDesigner(s)Junko KawanoWriter(s)Junko KawanoComposer(s)Junichi YoshidaPlatform(s)Nintendo DSReleaseJP: March 19, 2008NA: September 23, 2008EU: February 6, 2009Genre(s)Adventure, visual novelMode(s)Single-player Time Hollow (TIME HOLLOW 奪われた過去を求めて, Taimu Horou Ubawareta Kako o Motomete, lit. Time Hollow: Search for the Stolen Past)[1] is a Japanese adventure visual novel video game developed and published ...

Diamond Caverns

Diamond Caverns in Park City, Kentucky was discovered on July 14, 1859.[1] Tours are available year around; closed Thanksgiving, Christmas Eve, and Christmas. Tours last one hour and is a half mile round trip.[1] History On July 14, 1859, a slave of landowner Jessie Coats discovered a pit in the floor of a valley near the road to Mammoth Cave. The cave was given its name when the first visitor thought the calcite formations looked like diamonds.[1] The next day, a...

American Bulldog

Not to be confused with American Bully. For other bulldogs, see Bulldog (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: American Bulldog – news · newspapers · books · scholar · JSTOR (November 2023) (Learn how and when to remove this template message) Dog breedAmerican BulldogAmerican Bulld...

Kembali kehalaman sebelumnya