|
7
 「七」の筆順 「七」の筆順
7(七、漆、質、柒、しち、ひち、なな、ななつ、なー)は、自然数また整数において、6の次で8の前の数である。
英語では、基数詞でseven (セブン)、序数詞ではseventh。
読み
「七」の訓読みは「なな」、音読みは「しち」である。だが、「しち」という読みが言いにくく、また一(いち)、四(し)、八(はち)と聞き間違いをしやすいことから、他の数字なら音読みする文脈でも訓読みすることが多い(70〈ななじゅう〉など)。ただし、「7月(しちがつ)」、「7時(しちじ)」は、聞き間違いを意識的に排除する場合を除き、音読みされることが多い。名数では、他の数字同様、後に続く語が音読みか訓読みかによって読みが決まる(「七福神〈しちふくじん〉」「七草〈ななくさ〉」など)が、希に、後に音読みが続くにもかかわらず訓読みするものもある(「七不思議〈ななふしぎ〉」など)。
七(しち)を「ひち」と発音する方言もある。例えば岐阜県の「七宗町」の読みは「ひちそうちょう」と公式に定められている。
金銭証書などで間違いを防ぐため「漆」ないし「柒」を用いることがある。
性質
- 7 は4番目の素数である。1つ前は5、次は11。
- 7 = 7 + 0 × i (iは虚数単位)
- a + 0 × i (a > 0)で表される2番目のガウス素数。1つ前は3、次は11。
- 7 = 23 − 1
- 3番目のメルセンヌ数である。1つ前は3、次は15。
- 7 = 23 − 13
- 7 = 8 − 1
- p = 7 のときの 2p − 1 で表される 27 − 1 = 127 は4番目のメルセンヌ素数である。1つ前は5、次は13。
- 7 = 21 × 31 + 1
- 2番目の七角数である。1つ前は1、次は18。
- 1/7 = 0.142857… (下線部は循環節で長さは6)
- (5, 7) は2番目の双子素数。1つ前は(3, 5)、次は(11, 13)。
- (3, 5, 7) は唯一の (p , p + 2 , p + 4) 型の三つ子素数。
- (5, 7, 11, 13) は最小の四つ子素数。次は(11, 13, 17, 19)。
- 最小の 8n − 1 型の素数である。この類の素数は x2 − 2y2 と表せるが、7 = 32 − 2 × 12 である。次は23。
- 7 = 22 + 3
- 7 = 22 + 12 + 12 + 12 であり、4個の平方数の和で表せる。3個以下の平方数の和では表せない最小の自然数である。
- 5番目のトリボナッチ数である。1つ前は4、次は13。
- 4番目のリュカ数である。1つ前は4、次は11。
- 22/7 は円周率の比較的良い近似値である。値は 3.14285714… となる。これに関連して、7月22日は円周率近似値の日となっている。
- 平面図形である正七角形は、折り紙による作図ができても定規とコンパスによる作図ができない最小の正多角形である。次は正九角形。(オンライン整数列大辞典の数列 A004169)
- 正2mFaFb…Fc角形(Fa , Fb , … ,Fc は全て異なるフェルマー素数、m は非負整数)は定規とコンパスのみで作図することができる。
- 1から7までの7個全てで割り切れる、最小の数は[1,2,3,4,5,7] = 420 である。
- トーラス(円環)上の図表は、7色で彩色可能である(四色定理)。
- 最初の7つの素数の平方和は 666 になる。
22 + 32 + 52 + 72 + 112 + 132 + 172 = 666
- 7 を含むピタゴラス数は 72 + 242 = 252 である。
- 九九では 1 の段で 1 × 7 = 7(いんしちがしち)、7 の段で 7 × 1 = 7(しちいちがしち)と2通りの表し方がある。
- 7 までの自然数の和は完全数28になる。1 + 2 + 3 + 4 + 5 + 6 + 7 = 28
- ルネ・トムの提唱したのカタストロフの種類は全部で7である。
- 7! = 1 × 2 × 3 × 4 × 5 × 6 × 7 = 5040
- 7 × 8 × 9 × 10 = 5040 、7! は 7 から 10 の積に等しい。
- 7! − 1 = 5039
- 7! + 1 = 5041 = 712 より合成数である。
- 7# − 1 = 2 × 3 × 5 × 7 − 1 = 209 = 11 × 29 となり、初めて n# − 1 の形において合成数となる n である。(n# は素数階乗、つまり n 以下の素数の総乗)
- 7 = 20 + 21 + 22
- a = 2 のときの a0 + a1 + a2 の値とみたとき1つ前は3、次は13。
- a0 + a1 + a2 の形で表せる2番目のメルセンヌ素数である。1つ前は3、次は31。
- a0 + a1 + a2 の形で表せる2番目のハーシャッド数である。1つ前は3、次は21。
- a0 + a1 + a2 の形で表せる2番目の素数である。1つ前は3、次は13。
- 2の累乗和とみたとき1つ前は3、次は15。
- 各位の和が7となるハーシャッド数は100までに2個、1000までに6個、10000までに18個ある。
- 7番目のハーシャッド数である。1つ前は6、次は8。
- 7を基とする最小のハーシャッド数である。次は70。
- 各位の和(数字和)が7となる最小の数である。次は16。
- 各位の平方和が49になる最小の数である。次は70。(オンライン整数列大辞典の数列 A003132)
- 各位の立方和が343になる最小の数である。次は70。(オンライン整数列大辞典の数列 A055012)
- 各位の積が7になる最小の数である。次は17。(オンライン整数列大辞典の数列 A034054)
- 異なる平方数の和で表せない 31個の数の中で4番目の数である。1つ前は6、次は8。
- 約数の和が7になる数は1個ある。(4) 約数の和1個で表せる5番目の数である。1つ前は6、次は8。
- 約数の和が奇数になる3番目の奇数である。1つ前は3、次は13。
- 7 = 1 + 6
- 連続してある数に対して約数の和を求めていった場合3個の数が7になる。7より小さい数で3個ある数はない。1つ前は4 (2個)、次は8 (4個)。いいかえると
 を満たす n が3個あるということである (ただし σ は約数関数)。(参照オンライン整数列大辞典の数列 A241954) を満たす n が3個あるということである (ただし σ は約数関数)。(参照オンライン整数列大辞典の数列 A241954)
- 最初の 4n + 3 型の素数である。次は11。
- 幸運数となる3番目の数である。1つ前は3、次は9。(オンライン整数列大辞典の数列 A000959)
- 唯一の幸運数かつ安全素数である。
- 3番目の幸運数かつリュカ数の要素である。1つ前は3。
- 最小の 4n + 3 型の幸運数である。次は15。
- 累乗数はもちろん1にもなり得ない2番目の幸運数である。1つ前は3、次は13。
- 7 = 42 − 32 = (4 + 3) × (4 − 3)
- 7 = 32 − 2
- 以下のような無限多重根号の式で表せる。
 , , 
7の倍数の見分け方
- 「十の位以上の数 (10で除した商)」から「一の位の数 (10で除した剰余) の2倍を引いたもの」が7の倍数ならば、元の数は7の倍数である[2]。例として693の場合、693 = 69×10 + 3 であり、69 - 2×3 = 63 が7の倍数であることから、7の倍数であると判定できる。実際、693 = 7×99 なので7の倍数である。
- 十進数では、12(=3×4)以下の数のうち、7の倍数だけが「一の位」「数字和」「下P桁がabc」「ゾロ目」のどれも使えず、「M×一桁数」で一の位が1になる数を探す方法になる。十進数では7×3=21なので、一の位に2を掛けて元数を10で割った商から減じ、1桁になるまで続ける。結果が 0 か 7 か −7[注 1]なら、元数は7で割り切れる。
- 例1:259 → 25 - 9×2 = 7 → 259は7の倍数 (259 = 7 × 37)。
- 例2:2023 → 202 - 3×2 = 196
00000196 → 19 - 6×2 = 7 → 2023、196はどちらも7の倍数 (2023 = 7 × 289、196 = 7 × 28)。
- 桁数の多い十進数において、ある整数が7の倍数であるかどうかを判定する方法の一つとして、いくつか挙げられる
- 1001 = 7 * 11 * 13 だから 1000 = 1001 - 1 = ( 7 * 11 * 13 ) - 1
- ここから、元の数を3桁ごとに区切り、得られた数を右から順に交互に加減算を行い、奇数番目の和と偶数番目の和の差を計算する。
差として得られた数を7で除した剰余が元の数を7で除した剰余に一致するので、この剰余が0であれば元の数が7の倍数であると判別できる。
- たとえば 元の数を1234567890123 とした場合、
- 1234567890123 → 右から3桁ごとに「1」「234」「567」「890」「123」に分ける
→ 奇数番目の和と偶数番目の和
0000 (奇数番目) 1 + 567 + 123 = 691 、 (偶数番目) 234 + 890 = 1124
→ 2つの差は 691 - 1124 = -433 = (-1) * ( 7 * 62 + 1 )
→ 元の数 (1234567890123) を7で除した剰余は 1となり、7の倍数ではない。( 1234567890123 = 176366841446 × 7 + 1 )
- 1,000,000と100を 7 で除した剰余がそれぞれ 1 と 2 であることを応用した方法
- まず、ある元の数を「下から7桁目以降の数」と「下から6桁の数」とに区切り、得られた2つの数字をそれぞれ「下2桁(C)」「中2桁 (3~4桁目、B)」「5桁目以降(A)」の3つに分け、「5桁目以降」の数字(A)同士、「中2桁」の数字(B)同士、「下2桁」の数字(C)同士、各々を加えた3つの数(AA、BB、CC)を求める。次に、この3つの数をそれぞれ7で除した"剰余"を求め、「AAの"剰余"の4倍、BBの"剰余"の2倍、CCの"剰余"、この3つを加えた和」の4つの数を求める。最後に得られた和を更に7で除し、その剰余を求めると、元の数を7で除した剰余に一致する。従って、この剰余が0であれば元の数が7の倍数であると判別できる。
- たとえば 元の数を1234567890123 とした場合、
- 1234567890123 → 右から6桁ごとに「1234567」と「890123」に分ける
→ 「下2桁(C)」「中2桁 (B)」「5桁目以降(A)」に分け、桁の大きい方から順(A,B,C の順)に「 123, 45, 67 」 と「89, 01, 23 」に区分けする
→ それぞれ加える
0000(AA) 123 + 89 = 212, (BB) 45 + 01 = 46, (CC) 67 + 23 =90
→ "剰余"を求める
0000(AA) 212 mod 7 = 2, (BB) 46 mod 7 = 4, (CC) 90 mod 7 = 6
→ それぞれ指定の係数を掛けて足す
- 00002×4 + 4×2 + 6 = 22, ∴ 22 mod 7 = 1
→ 元の数 (1234567890123) を7で除した剰余は 1となり、7の倍数ではない。( 1234567890123 = 176366841446 × 7 + 1 )
- 十二進数での5の倍数と7の倍数の判定も、十進数での7の倍数の判定と同様になる。十二進数では5×5=21、7×7=41なので、7の倍数の場合は一の位に4を掛けて元数を10で割った商から減じ、1桁になるまで続ける。
- 例1:115 → 5×4 = 18、11 - 18 = -7。
- 例2:1054 → 4×4 = 14、105 - 14 = B1。B1 → 1×4 = 4、B - 4 = 7。
その他 7 に関すること
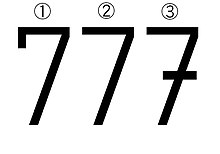 筆記時、日本や台湾や韓国では1番のように書かれることが多い。その他の国では2番のように書くのが一般的で、数字の1との区別のために3番のように線を入れたりする。日本人が1を強調して書くときに、縦棒線の上にカギを付けることがあるが、その字形は欧米では7と認識される可能性がある。 筆記時、日本や台湾や韓国では1番のように書かれることが多い。その他の国では2番のように書くのが一般的で、数字の1との区別のために3番のように線を入れたりする。日本人が1を強調して書くときに、縦棒線の上にカギを付けることがあるが、その字形は欧米では7と認識される可能性がある。
 電卓やデジタル時計等の7セグメントディスプレイでの表記方法は2通りある 電卓やデジタル時計等の7セグメントディスプレイでの表記方法は2通りある
言語
- 7の接頭辞:sept(拉)、hepta(希)
- 7倍、7重をセプテュプル(セプタプル、septuple)という。
- 七種競技 (heptathlon) 等。
- 七重奏のことをセプテット (septet) と言う。
- 7を表すヘブライ数字はザイン。
- 24/7 (twenty-four seven) は、24時間・週7日間を意味し、転じて always(いつも)、24時間営業年中無休という意味を持つ。
7番目のもの
宗教に関する7
天文に関する7
遊びに関する7
パズルに関する7
その他
7個1組の概念
符号位置
| 記号 |
Unicode |
JIS X 0213 |
文字参照 |
名称
|
| 7 |
U+0037 |
1-3-22 |
7
7 |
DIGIT SEVEN
|
| 7 |
U+FF17 |
1-3-22 |
7
7 |
FULLWIDTH DIGIT SEVEN
|
| ⁷ |
U+2077 |
- |
⁷
⁷ |
SUPERSCRIPT SEVEN
|
| ₇ |
U+2087 |
- |
₇
₇ |
SUBSCRIPT SEVEN
|
| ৺ |
U+09FA |
- |
৺
৺ |
BENGALI CURRENCY NUMERATOR SEVEN
|
| ༰ |
U+0F30 |
- |
༰
༰ |
TIBETAN DIGIT HALF SEVEN
|
| ፯ |
U+136F |
- |
፯
፯ |
ETHIOPIC DIGIT SEVEN
|
| ᧗ |
U+19D7 |
- |
᧗
᧗ |
NEW TAI LUE THAM DIGIT SEVEN
|
| Ⅶ |
U+2166 |
1-13-28 |
Ⅶ
Ⅶ |
ROMAN NUMERAL SEVEN
|
| ⅶ |
U+2176 |
1-12-28 |
ⅶ
ⅶ |
SMALL ROMAN NUMERAL SEVEN
|
| ⑦ |
U+2466 |
1-13-7 |
⑦
⑦ |
CIRCLED DIGIT SEVEN
|
| ⑺ |
U+247A |
- |
⑺
⑺ |
PARENTHESIZED DIGIT SEVEN
|
| ⒎ |
U+248E |
- |
⒎
⒎ |
DIGIT SEVEN FULL STOP
|
| ⓻ |
U+24FB |
1-6-63 |
⓻
⓻ |
DOUBLE CIRCLED DIGIT SEVEN
|
| ❼ |
U+277C |
1-12-8 |
❼
❼ |
DINGBAT NEGATIVE CIRCLED DIGIT SEVEN
|
| ➆ |
U+2786 |
- |
➆
➆ |
DINGBAT CIRCLED SANS-SERIF DIGIT SEVEN
|
| ➐ |
U+2790 |
- |
➐
➐ |
DINGBAT NEGATIVE CIRCLED SANS-SERIF DIGIT SEVEN
|
| ㆘ |
U+3198 |
- |
㆘
㆘ |
IDEOGRAPHIC ANNOTATION SEVEN MARK
|
| ㈦ |
U+3226 |
- |
㈦
㈦ |
PARENTHESIZED IDEOGRAPH SEVEN
|
| ㊆ |
U+3286 |
- |
㊆
㊆ |
CIRCLED IDEOGRAPH SEVEN
|
| 七 |
U+4E03 |
1-28-23 |
七
七 |
CJK Ideograph, number seven
|
| 柒 |
U+67D2 |
2-14-48 |
柒
柒 |
CJK Ideograph, number seven
|
| 漆 |
U+6F06 |
1-28-31 |
漆
漆 |
CJK Ideograph, number seven
|
| 𐄍 |
U+1010D |
- |
𐄍
𐄍 |
AEGEAN NUMBER SEVEN
|
| 𐡞 |
U+1085E |
- |
𐡞
𐡞 |
IMPERIAL ARAMAIC NUMBER SEVEN
|
| |
U+1091C |
- |
𐤜
𐤜 |
PHOENICIAN NUMBER SEVEN
|
| 𐩆 |
U+10A46 |
- |
𐩆
𐩆 |
KHAROSHTHI DIGIT SEVEN
|
| 𐪃 |
U+10A83 |
- |
𐪃
𐪃 |
OLD SOUTH ARABIAN NUMBER SEVEN
|
| 𐭟 |
U+10B5F |
- |
𐭟
𐭟 |
INSCRIPTIONAL PARTHIAN NUMBER SEVEN
|
| 𐹦 |
U+10E66 |
- |
𐹦
𐹦 |
RUMI DIGIT SEVEN
|
| 𝍦 |
U+1D366 |
- |
𝍦
𝍦 |
COUNTING ROD UNIT DIGIT SEVEN
|
| 🄈 |
U+1F108 |
- |
🄈
🄈 |
DIGIT SEVEN COMMA
|
| 𝟟 |
U+1D7DF |
- |
𝟟
𝟟 |
MATHEMATICAL DOUBLE-STRUCK DIGIT SEVEN
|
| 𝟽 |
U+1D7FD |
- |
𝟽
𝟽 |
MATHEMATICAL MONOSPACE DIGIT SEVEN
|
| 𝟕 |
U+1D7D5 |
- |
𝟕
𝟕 |
MATHEMATICAL BOLD DIGIT SEVEN
|
| 𝟩 |
U+1D7E9 |
- |
𝟩
𝟩 |
MATHEMATICAL SANS-SERIF DIGIT SEVEN
|
| 𝟳 |
U+1D7F3 |
- |
𝟳
𝟳 |
MATHEMATICAL SANS-SERIF BOLD DIGIT SEVEN
|
他の表現法
脚注
注釈
- ^ マーチン・ガードナー『数学ゲーム II』講談社〈ブルーバックス〉、1974年。B-249。 −7 についての言及はないが、14 などが 7 で割れることから、含めておくべきであろう。
- ^ 1998年(平成10年)2月2日から。それまでは3桁または5桁であった。
出典
- ^ 『魅惑と驚きの「数」たち』 イアン・スチュアート著 P104
- ^ 数学セミナー2003年3月号P59
- ^ “年号一覧表”. www.kumamotokokufu-h.ed.jp. 2022年3月8日閲覧。
関連項目
ウィキメディア・コモンズには、 7に関連するカテゴリがあります。
外部リンク
|
|