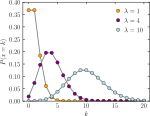
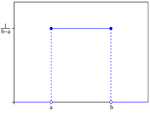
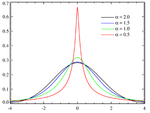
Розподіл імовірностей
|
Read other articles:

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: アークザラッドII – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2019年12月) アークザラッドII ゲーム ゲームジャン�...

Map of Samoa This article shows a list of cities, towns and villages in Samoa. List Main townships Apia, capital of Samoa situated on Upolu island. Salelologa, main 'township' & ferry terminal on Savai'i island. Villages Afega Afiamalu Alafua Alamagoto Aleipata Aleisa Amaile Amouli Aopo Apai Apolima Tai Apolima Uta Asaga Asau Auala A'ufaga Aele Elisefou Faiaai Faatoia Faga Fagali'i Fagaloa Fagamalo Falealili Falealupo Faleasiu Faleatiu Falefa Falelatai Falelima Fale'olo Falease'ela, Lefag...

Standing committee of the Senate of the Philippines Committee on Public Information and Mass Media19th CongressHistoryNew session startedJuly 25, 2022 (2022-07-25)LeadershipChairmanRobinhood Padilla (PDP-Laban) since 2022 Minority LeaderKoko Pimentel (PDP-Laban) since 2022 StructureSeats13 membersPolitical groupsMajority (12) PDP–Laban (3) Independents (1) Pwersa ng Masang Pilipino (1) Lakas (1) Nacionalista (3) NPC (3) Minori...

Democratic member of the U.S. House of Representatives from Pennsylvania From Volume 13 (1921) of Encyclopedia of Pennsylvania Biography John Reilly (February 22, 1836 – April 19, 1904) was a Democratic member of the U.S. House of Representatives from Pennsylvania. Biography John Reilly was born in Abnerville, Indiana County, Pennsylvania.[1] He received home instruction and attended the public schools. He entered the service of the Pennsylvania Railroad, on April 10, 1854. He was a...

Kho báu bị đánh cắp Poster chiếu rạpĐạo diễnGeorge ClooneySản xuấtGeorge ClooneyGrant HeslovKịch bảnGeorge ClooneyGrant HeslovDựa trênThe Monuments Mencủa Robert M. Edsel và Bret WitterDiễn viên George Clooney Matt Damon Bill Murray John Goodman Jean Dujardin Bob Balaban Hugh Bonneville Cate Blanchett Âm nhạcAlexandre DesplatQuay phimPhedon PapamichaelDựng phimStephen MirrioneHãng sản xuấtFox 2000 PicturesSmokehouse PicturesStudio Babelsberg Ph�...

Achille van Acker Primer ministro de Bélgica 12 de febrero de 1945-13 de marzo de 1946Monarca Leopoldo IIICarlos (regente)Predecesor Hubert PierlotSucesor Paul-Henri Spaak 31 de marzo de 1946-3 de agosto de 1946Monarca Leopoldo IIICarlos (regente)Predecesor Paul-Henri SpaakSucesor Camille Huysmans 23 de abril de 1954-26 de junio de 1958Monarca BalduinoPredecesor Jean Van HoutteSucesor Gaston Eyskens Información personalNombre en neerlandés Achille Honoré Van Acker Apodo Achiel Nacimiento ...

3rd episode of the 1st season of Randall and Hopkirk All Work and No PayRandall and Hopkirk (Deceased) episodeEpisode no.Season 1Episode 3Directed byJeremy SummersWritten byDonald JamesProduction code03Original air date5 October 1969 (1969-10-05)Guest appearances Alfred Burke Adrienne Corri Dudley Foster Noel Davis Episode chronology ← PreviousA Disturbing Case Next →Never Trust a Ghost List of episodes All Work and No Pay is the third episode of the 1969 ITC...

US television program The Sifl and Olly ShowScreenshot showing Sifl (left) and Olly (right).GenreSurreal comedyCreated byLiam Lynch and Matt CroccoStarringMatt Crocco and Liam LynchComposerLiam LynchCountry of originUnited StatesOriginal languageEnglishNo. of seasons3ProductionProducersLiam Lynch, Matt Crocco, and Michael TaylorCinematographySteve PriolaEditorsByron Glickfeld and Thomas G. OlsenRunning time30 minutesOriginal releaseNetworkMTVReleaseJuly 14, 1998 (July 14, 1998) –1...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2020) .يتم توفير الوصول العالمي في كوريتيبا الصورة وسائل النقل العام نظام والبرازيل.المعرقل (وتسمى أيضا حاجز، عقبة، أو عثرة) هو أي شيء قد يسبب انسداد وتشمل أنواع مخت

Teluk Deep Hanzi tradisional: 后海灣 Hanzi sederhana: 后海湾 Alih aksara Mandarin - Hanyu Pinyin: Hòuhǎi Wān Kejia (Hakka) - Romanisasi: Hiu4hoi3 Van1 Yue (Kantonis) - Jyutping: hau6 hoi2 waan1 nama alternatif Hanzi tradisional: 深圳灣 Hanzi sederhana: 深圳湾 Alih aksara Mandarin - Hanyu Pinyin: Shēnzhèn Wān Yue (Kantonis) - Jyutping: sam1 zan3 waan1 Deep Bay adalah sebuah teluk di antara Yuen Long, Hong Kong, dan Kota Shenzhen.[1] Teluk ini dikenal sebagai Hau Hoi W...

French sculptor (1730–1809) Portrait of Pajou by Adélaïde Labille-Guiard.[1] Bust of Michel-Jean Sedaine, 1775, The Victoria and Albert Museum, London. Mercury, 1780. Augustin Pajou (19 September 1730 – 8 May 1809) was a French sculptor, born in Paris. At eighteen he won the Prix de Rome, and at thirty exhibited his Pluton tenant Cerbère enchaîné (now in the Louvre). Selected works Pajou's portrait busts of Buffon and of Madame du Barry (1773), and his statuette of Bossuet (a...

Jean-Baptiste DelafosseJean-Baptiste Delafosse, Vue des tentes turques au parc Monceau, d'après CarmontelleBiographieNaissance 1721ParisDécès 1er février 1806[1]Ancien 10e arrondissement de ParisNom de naissance Jean-Baptiste Joseph DelafosseNationalité FrançaiseActivité graveur, pastelisteAutres informationsMaître Étienne Fessardmodifier - modifier le code - modifier Wikidata Jean-Baptiste Delafosse est un graveur d'interprétation et de cartographie (eau-forte et burin), également...

1983 studio album by Waylon JenningsWaylon and CompanyStudio album by Waylon JenningsReleasedSeptember 1983GenreCountryoutlaw countryLength32:02LabelRCA VictorProducerWaylon JenningsWaylon Jennings chronology Take It to the Limit(1983) Waylon and Company(1983) Never Could Toe the Mark(1984) Singles from Waylon and Company The ConversationReleased: October 22, 1983 I May Be Used (But Baby I Ain't Used Up)Released: March 3, 1984 Professional ratingsReview scoresSourceRatingAllmusic[...

Hospital in Ein Karem, JerusalemHadassah Medical CenterHadassah in Ein Karem, Jerusalem, the second campus of the Hadassah Medical CenterGeographyLocationEin Karem, JerusalemCoordinates31°47′50″N 35°14′31″E / 31.79722°N 35.24194°E / 31.79722; 35.24194OrganisationCare systemPrivateTypeTeaching, District GeneralAffiliated universityHebrew University of JerusalemPatronHadassah Women's Zionist Organization of AmericaServicesEmergency departmentYesBeds1,029[...

For other uses, see Jabaquara (disambiguation). Jabaquara Intermunicipal Terminal is an intermunicipal bus terminal in São Paulo, Brazil. Along with the Tietê Bus Terminal and the Palmeiras-Barra Funda Intermodal Terminal, it is one of the most important bus terminals in the State of São Paulo.[1] tel.11 5060-4275 of ambulatory. References ^ Jabaquara Intermunicipal Terminal on Socicam's website (Portuguese) External links Official website of the Socicam, the company that administe...

Esanatoglia EsanatogliaTọa độ: 43°15′B 12°57′Đ / 43,25°B 12,95°Đ / 43.250; 12.950 Quốc gia ÝThủ phủEsanatoglia Độ cao495 m (1,624 ft) • Mật độ45/km2 (120/mi2)Múi giờUTC+1, UTC+2 Mã bưu chính62023Mã điện thoại0737Mã ISTAT043016Danh xưngesanatogliesiThánh bổn mạngSanta AnatoliaTrang webhttp://www.esanatoglia.sinp.net Esanatoglia là một đô thịthuộc tỉn...

Four-year institutions Map of full NCAA Division II Independent schools NCAA Division II independent schools are four-year institutions that compete in college athletics at the NCAA Division II level, but do not belong to an established athletic conference for a particular sport. These schools may however still compete as members of an athletic conference in other sports. A school may also be fully independent, and not belong to any athletic conference for any sport at all. The reason for ind...

The correct title of this article is #osnrap. The omission of the # is due to technical restrictions. 2019 studio album by OSN#osnrapStudio album by OSNReleased30 April 2019GenreMandopop, hip hop, rapLength31:14LabelSKR Presents #osnrap is the debut studio album of Taiwanese rapper and singer OSN. It was released on 30 April 2019 by SKR Presents and contains a total of 10 tracks.[1] The title of the album refers to the hashtag he use in his Instagram posts to share his music.&...

Company specializing in pickled products Vlasic PicklesFounded1942FounderFrank VlasicHeadquartersParsippany, New Jersey (Produced in Imlay City, Michigan), United StatesProductsPickled cucumbers Relish OwnerConagra Brands[1]Websitevlasic.com Vlasic Pickles Vlasic is an American brand of pickles that is currently owned by Conagra Brands. Since its introduction in 1942, it has become one of the most popular pickle brands in the United States. History Franjo Frank Vlašić, a Bosnian Cro...

This article is about a ski resort in Maine, USA. For the mountain by the same name, see Sugarloaf Mountain (Franklin County, Maine). For the ski resort in Campbellton, New Brunswick, see Sugarloaf Provincial Park. Ski resort in Maine, USA SUGARLOAFSugarloaf LogoLocationCarrabassett Valley,Franklin County, Maine United StatesNearest major cityFarmingtonCoordinates45°01′53″N 70°18′47″W / 45.03139°N 70.31306°W / 45.03139; -70.31306StatusOperatingOwnerBoy...





![{\displaystyle F(x)=\Pr \left[X\leq x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a38abba897b79daf3a91bf12d0cd42f5aaf345a9)
![{\displaystyle \Pr \left[a\leq X\leq b\right]=\int _{a}^{b}f(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cddb084adf4086a239bbaf753ad0566940150389)
![{\displaystyle F(x)=\Pr \left[X\leq x\right]=\sum _{x_{i}\leq x}p(x_{i})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fa5fd3aee9c5275e9352893b908071261d67299)